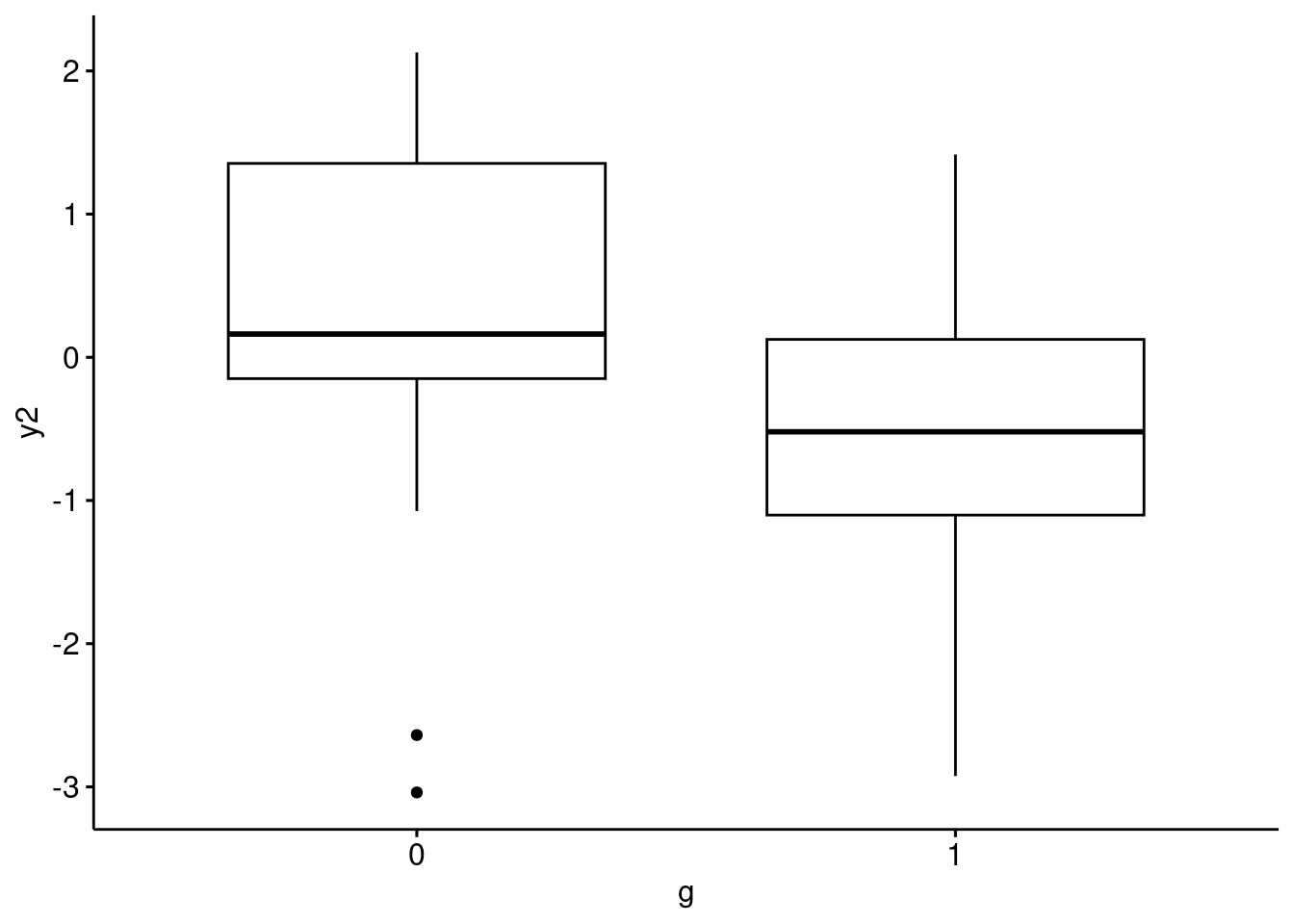12 Auswerten: Modellieren – Forschungsprojekt

12.1 Lernsteuerung

12.1.1 Lernziele

Sie können die Modellformel Ihrer Forschungsfrage nennen.
Sie können Ihre Modellformel (korrekt) in R spezifizieren.
Sie können Ihr Modell in R berechnen und die Ausgabe interpretieren.

12.1.2 Benötigte R-Pakete

library(tidyverse)
library(easystats)
library(ggstatsplot)  # Visualisierung
library(ggpubr)  # Visualisierung
library(rstanarm)  # Bayes

12.1.3 Position im Lernpfad

Sie befinden sich im Abschnitt “Auswerten” in Abbildung 1.2. Behalten Sie Ihren Fortschritt im Projektplan im Blick, s. Abbildung 1.3.

12.1.4 Weitere Lernmaterialien

12.1.4.1 Skript Bayes-Modellierung 📖

Die Grundlagen der statistischen Modellierung mit einem Fokus auf Bayes-Modellen können Sie hier nachlesen.

12.1.4.2 Videos 📽️

In einigen Playlists des Autors finden Sie Videos passend zu diesem Kapitel:

12.1.5 Überblick

In diesem Kapitel sind die grundlegenden Verfahren zur Modellierung und inferenzstatistischen Absicherung Ihrer Forschungsfragen angerissen. Die Darstellung zielt auf ein “so-geht’s” ab, nicht auf eine vollständige Darstellung aller Auswertungsmöglichkeiten.

Modellierung bedeutet, dass Sie Ihre Forschungsfrage(n) bzw. Hypothese(n) in ein statistisches Modell überführen. Praktisch gesehen heißt das, dass Sie ein Regressionsmodell der Art AV ~ UV1 + UV2 + ... aufstellen, s. Kapitel 10.7.

Welche bzw. wie viele UV sollte man in ein (Regressions-)modell aufnehmen? Nehmen Sie alle Variablen auf, von denen Sie annehmen, dass es Ursachen Ihrer AV sind. Berechnen Sie also nicht für jede UV ein eigenes Modell, sondern packen Sie alle UV in ein einziges Regressionsmodell. Das beinhaltet auch Konfundierungsvariablen und sonstige Ursachen der AV, die für Ihre Fragestellung nicht so interessant sind (wie Alter und Geschlecht), aber helfen, zu genaueren Schätzungen zu kommen. Variablen mit anderen kausalen Funktionen, wie Mediatorvariablen, sollten nicht in Ihr Modell aufgenommen werden, mit dem Sie den Effekt der UV auf die AV untersuchen.

Inferenzstatistik ordnet den Hypothesen eine Wahrscheinlichkeit zu und weist Punktschätzern einen Schätzbereich zu, s. Kapitel 10.7. Kurz gesagt: Inferenzstatistik bestimmt die Ungewissheit einer Schätzung.

Praktisch ist nicht viel zu tun für die Inferenzstatistik: Ihr Modellierungsbefehl (wie stan_glm oder lm) bereitet schon die Inferenzstatistik für Sie vor. Mit Befehlen wie parameters oder summary können Sie Ihrem Modell einfach die inferenzstatistischen Kennwerte entlocken.

12.2 1 between-Variable, nur Nachher-Messung

12.2.1 Design

Sauer & Lustig (2023) untersuchten in einer Querschnittsstudie den Effekt des Wirkstoff Bringnixtin auf die fluide Intelligenz. Die Autoren nahmen an, dass der Wirkstoff den individuellen Wert der abhängigen Variable erhöhen würde.

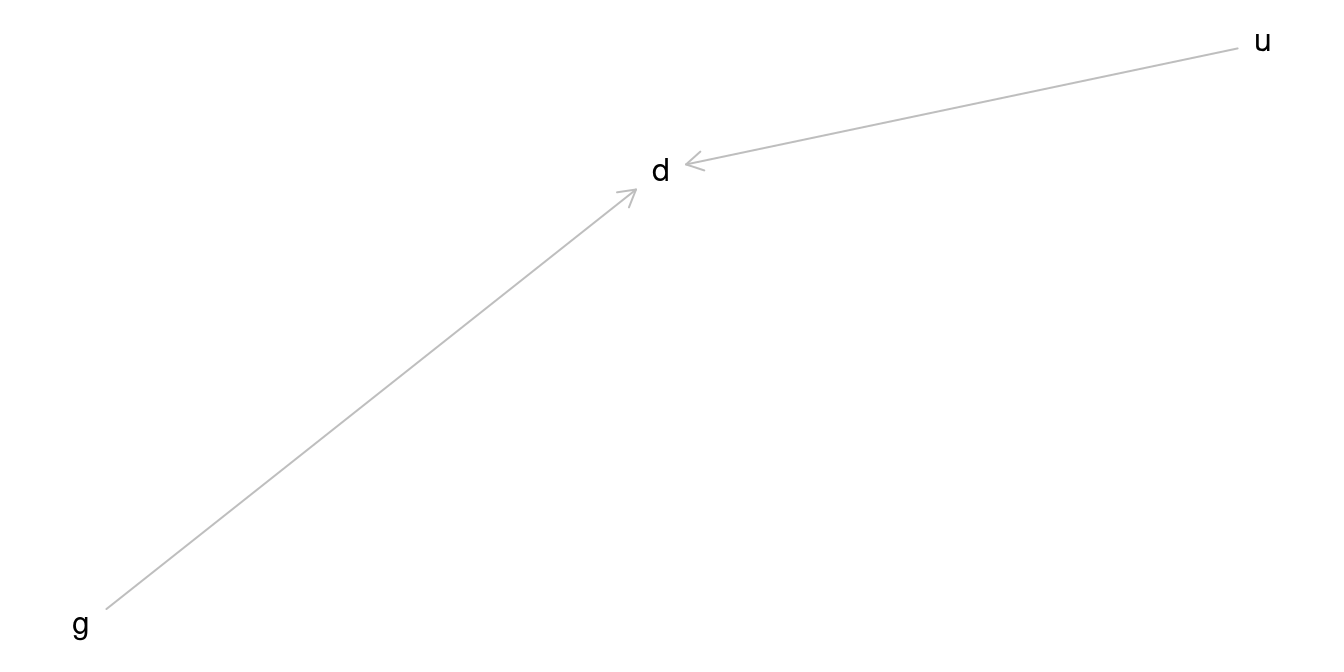
Der Ablauf (aus Sicht der Probandis) ist in Abbildung 12.1 dargestellt. Intro fasst die Begrüßung der Probandis inkl. Informed Consent sowie Erfassung von soziodemografischen Variablen zusammen. g.0 und g.1 sind die zwei Stufen der UV (g wie Gruppe), wobei g.0 die Kontrollgruppe kodiert (Placebo, also Zuckerpille, kein Wirkstoff,) und g.1 die zweite Stufe, d.h. die Experimentalgruppe (hohe Dosis Bringtnixtin). y2 ist die Messung der AV (d.h. nach Gabe von Bringtnixtin), d.h. ein Maß der fluiden Intelligenz. outro meint die Verabschiedung der Probanden sowie einige Fragen zu Compliance.

Die Hypothese lautet: $μ_{g .2} > μ_{g .1}$ .

In Worten:

Wir erwarten, dass der Mittelwert der Experimentalgruppe höher ist als der Mittelwert der Kontrollgruppe.

Abbildung 12.1: Ablaufdiagramm der Bringtnixtin-Studie

Der DAG des Experiments ist in Abbildung 12.2 dargestellt.

Abbildung 12.2: DAG für der Bringtnixtin-Studie

Hinweis

Im DAG Abbildung 12.2 ist u als Ursache von y2 angegeben. u steht hier stellvertretend für alle weiteren Ursachen von y2, vermutlich sind das sehr viele. Aber sie interessieren uns nicht. Daher können Sie u auch aus dem DAG weglassen. Streng genommen sollten Sie es sogar weglassen, denn im DAG zeigt man nur diejenigen Variablen, die für Ihre Hypothese von Belang sind. Da u keine Verbindung zum Pfad g -> y2 hat, brauchen wir es für die Bestimmung des Kausaleffekts nicht zu berücksichtigen. $◻$

Die Daten dieses Experiments sind hier zu beziehen:

d_bringtnixtin_path <- "https://raw.githubusercontent.com/sebastiansauer/fopra/main/data/d_bringtnixtin.csv"
d_bringtnixtin <- read_csv(d_bringtnixtin_path)

Die Autoren der Studie geben an, dass die Daten in z-Einheiten skaliert sind.

12.2.2 Deskriptive Analyse

d_bringtnixtin_summary <- 
d_bringtnixtin %>% 
  group_by(g) %>% 
  summarise(y2_mean = mean(y2),
            y2_sd = sd(y2))

Tabelle 12.1: Mittlere fluide Intelligenz nach der Bringtnixtin-Intervention in Abhängigkeit der Gruppe

ABCDEFGHIJ0123456789

g <dbl>	y2_mean <dbl>	y2_sd <dbl>
0	0.1917379	1.337211
1	-0.5722050	1.110908

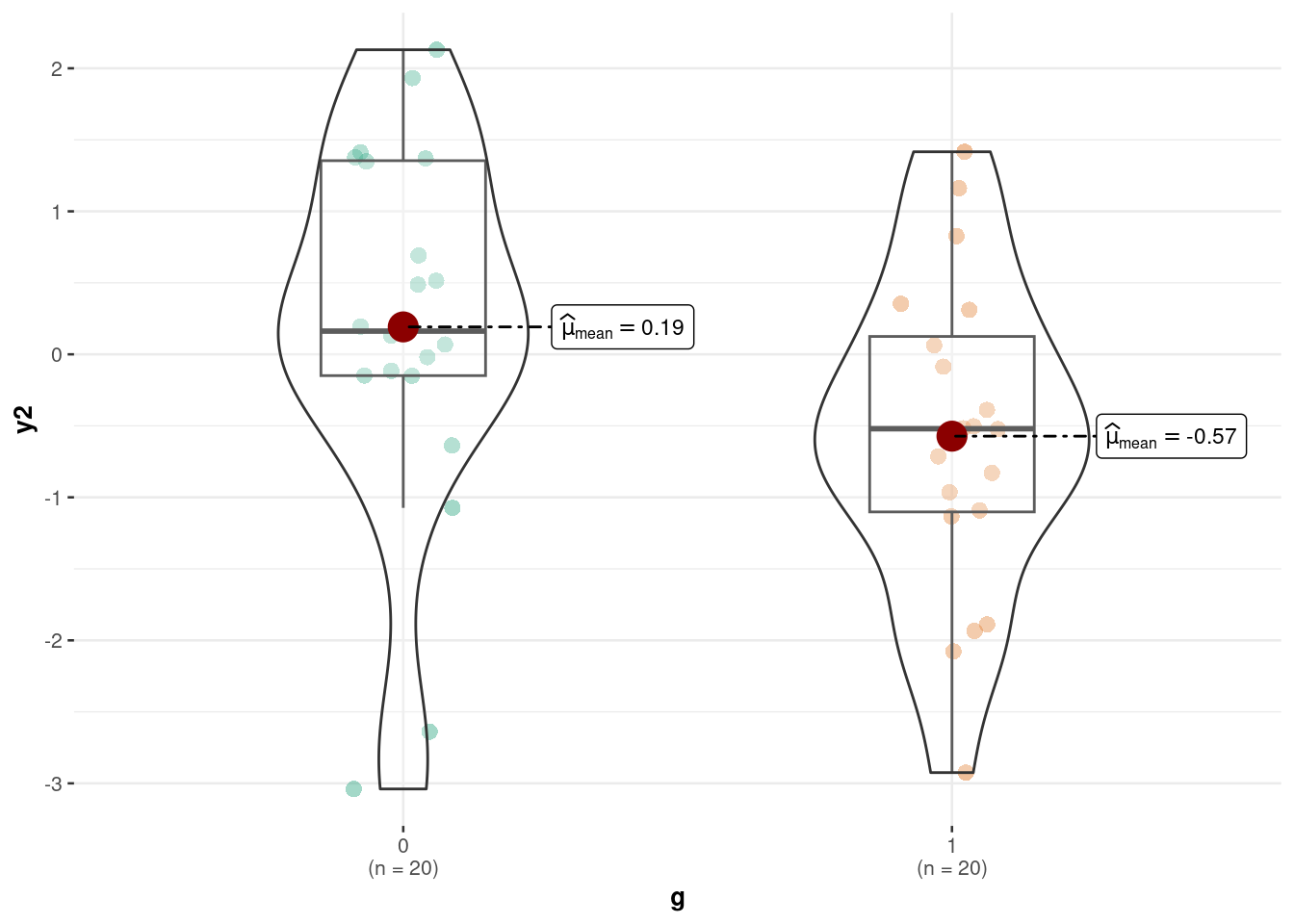
Die deskriptiven Kennwerte sind in Abbildung 12.3 bzw. Abbildung 12.3 visualisiert. Das sieht nicht gerade nach einem großen Effekt aus …¹

Mit ggstatsplot
Mit ggpubr

ggbetweenstats(
  data = d_bringtnixtin,
  x = g,
  y = y2,
  results.subtitle = FALSE  # keine Statistiken zeigen
)

Abbildung 12.3: Fluide Intelligenz (y2) nach der Bringtnixtin-Intervention. g=0: Kontrollgruppe (Placebo), g=1: Experimentalgruppe (hohe Dosis). Die vertikale Linie zeigt die Stärke des Effekts (entspricht dem Unterschied in den Mittelwerten der Gruppen)

ggboxplot(
  data = d_bringtnixtin,
  x = "g",
  y = "y2",
  add = "mean"
)

Abbildung 12.4: Fluide Intelligenz (y2) nach der Bringtnixtin-Intervention. g=0: Kontrollgruppe (Placebo), g=1: Experimentalgruppe (hohe Dosis).Die vertikale Linie zeigt die Stärke des Effekts (entspricht dem Unterschied in den Mittelwerten der Gruppen)

Sowohl das R-Paket ggstatsplot als auch das R-Paket ggpubr bieten ansprechende Datenvisualisierung.²

Der Gruppenunterschied ist der Effekt

Der Effekt einer UV bemisst sich am (mittleren) Unterschied in der AV zwischen den Gruppen.

12.2.3 Modellierung und Inferenz

Wir berechnen ein lineares Modell mit der Modellformel y2 ~ g.

12.2.3.1 Parameterschätzung

Die Ergebnisse unseres Modells m_bringtnixtin sind in Tabelle 13.5 zu sehen.

m_bringtnixtin <- stan_glm(y2 ~ g, 
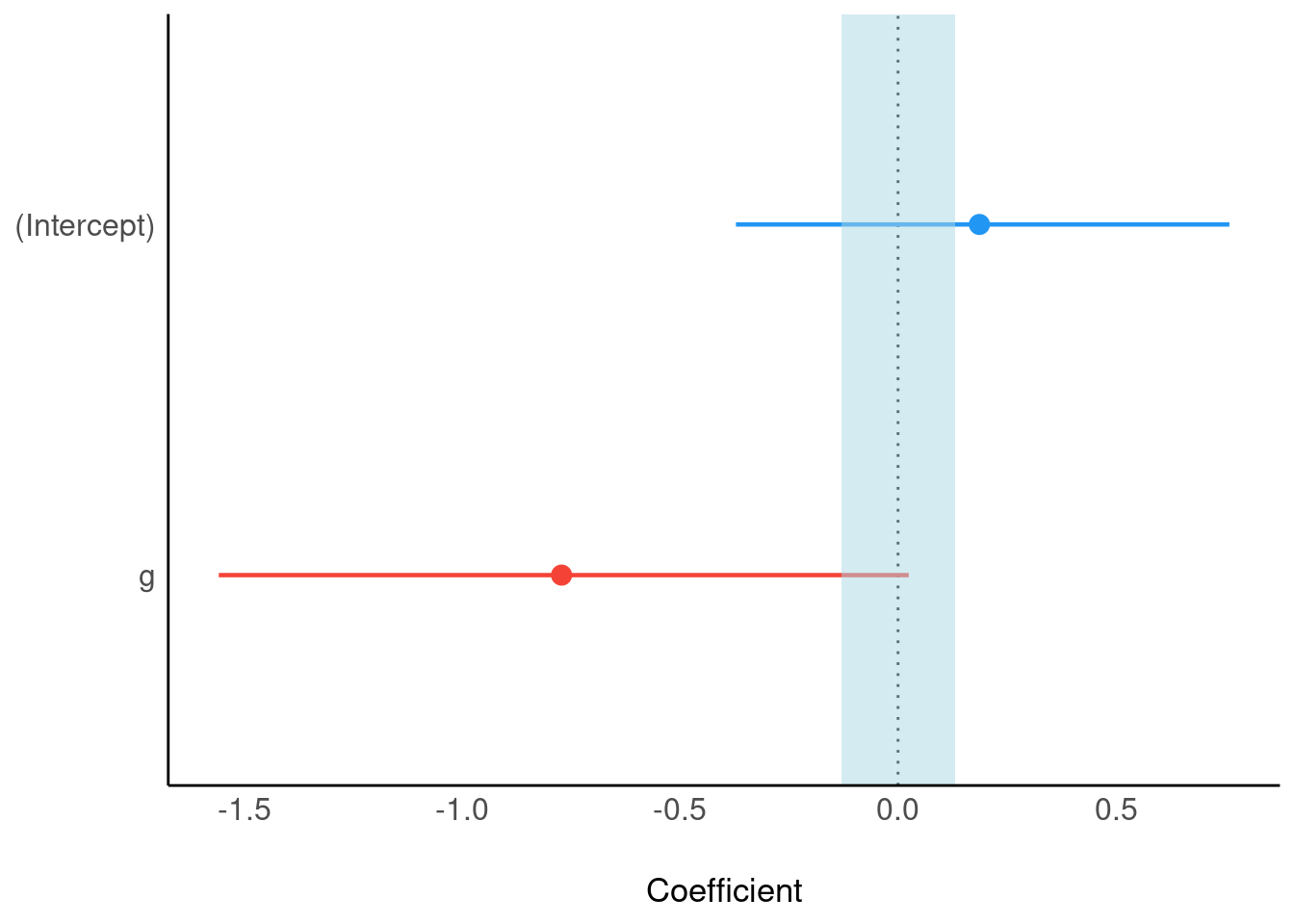
                           data = d_bringtnixtin)

parameters(m_bringtnixtin)

Tabelle 12.2: Parameter des Modells m_bringtnixtin

ABCDEFGHIJ0123456789

Parameter <chr>	Median <dbl>	CI <dbl>	CI_low <dbl>	CI_high <dbl>	pd <dbl>	Rhat <dbl>
(Intercept)	0.1872474	0.95	-0.3734893	0.7405634	0.74825	0.9994630
g	-0.7621084	0.95	-1.5172969	0.0207076	0.97275	0.9998109

Der Gruppenunterschied wird auf das -0.76 geschätzt; das ist der Punktschätzer der UV g. Wenn wir nur eine Zahl nennen dürften zu unserem Wissen zum Effekt von g, so wäre das unsere Zahl. Die Grenzen eines 95%-CI für die UV liegen bei -1.55 bzw. -0.01; diese beiden Werten markieren die Grenzen des Intervallschätzers. Dieser Bereich enthält die Null, vgl. Abbildung 12.5. Daher kann nicht ausgeschlossen werden, dass Bringtnixtin nix bringt. Anders gesagt: Die (strenge) Nullhypothese kann nicht verworfen werden. Der Wert Null ist ein plausibler Wert für den Parameter, da er im 95%-CI enthalten ist.

Hinweis

Ist der Wert Null NICHT im 95%-Schätzintervall enthalten, so heißt das, dass die Null(hypothese) verworfen werden.
Ist der Wert Null im 95%-Schätzintervall enthalten, so heißt das, dass die Null(hypothese) NICHT verworfen werden. $◻$

Die Punkt- und Intervallschätzer (95%-ETI) für Achsenabschnitt und Regressiongewicht von g sind in Abbildung 12.5 visualisiert.

Hinweis

Zur Erinnerung: Ein Punktschätzer schätzt einen (unbekannten) Wert in der Population auf einen einzelnen Wert (daher “Punkt”). Ein Interschätzer schätzt einen Wertebereich für diesen unbekannten Wert. $◻$

parameters(m_bringtnixtin) %>% plot(show_intercept = TRUE)

Abbildung 12.5: Parameter des Modells `m_bringtnixtin (95%-ETI)`; der ROPE ist als vertikaler blauer Balken markiert

👨‍🏫 Frau Professor Lustig, wie kann das sein, dass sich die Hypothese nicht bestätigt?

👩‍🏫 Herr Professor Sauer, auch ein negatives Ergebnis bringt die Wissenschaft weiter.

12.2.3.2 Praktisch-Null-Hypothese (ROPE)

Definition 12.1 (Praktisch-Null-Hypothese (ROPE)) Kurz gesagt wird beim ROPE geprüft, welcher Anteil des Posteriori-Intervalls zu einem Bereich “vernachlässigbar kleiner” Parameterwerte bewegt (Kruschke, 2018). $◻$

Mit dem ROPE-Verfahren kann man eine “Praktisch-Null-Hypothese” testen, also ob ein Bereich um die Null herum, also “Null plus-minus ein bisschen” im Hauptbereich im Hauptbereich (95%-KI) enthalten ist.

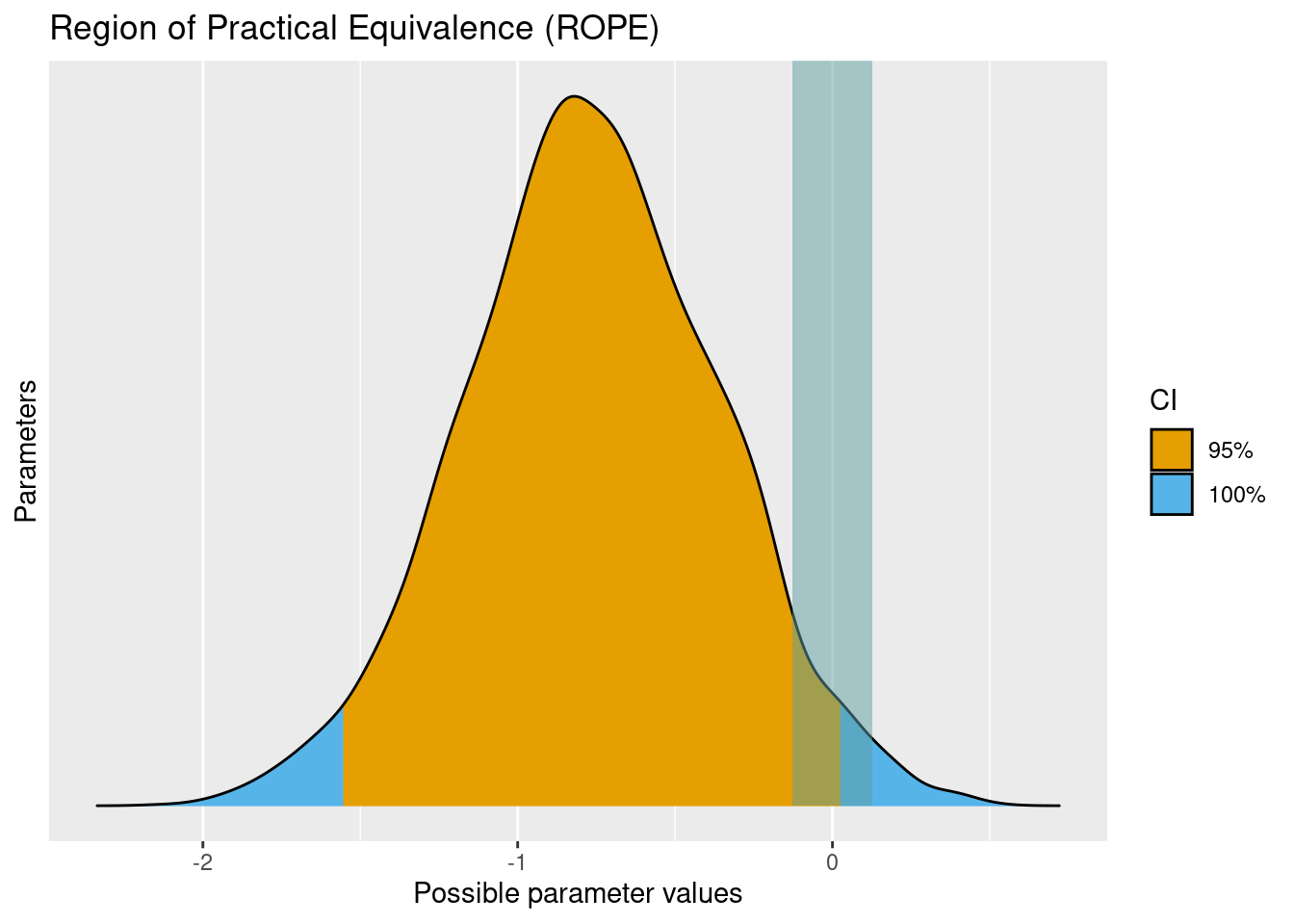
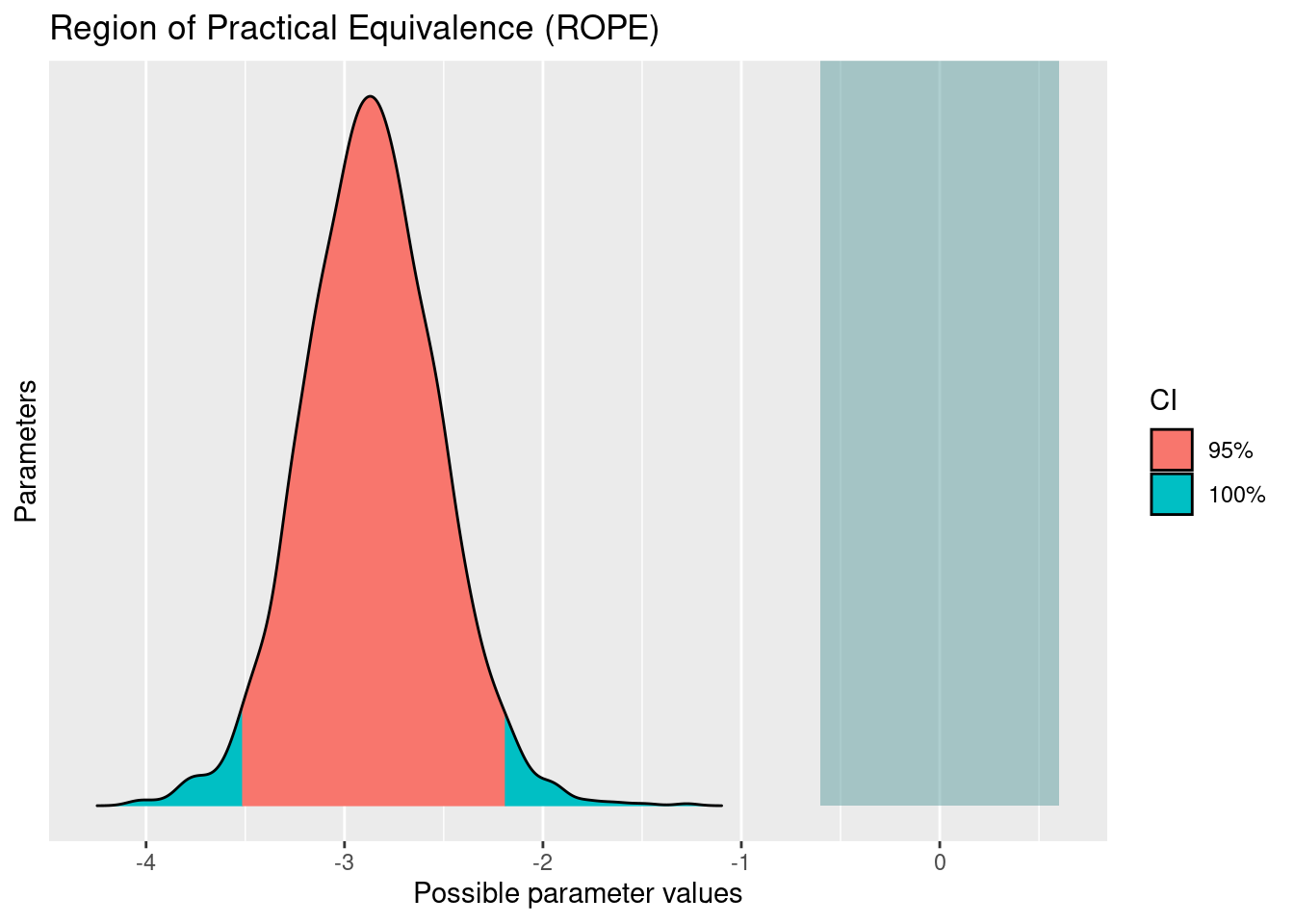
Schauen wir uns die Umsetzung in R anhand des Beispiels zu Bringtnixtin an: rope(m_bringtnixtin), s. Tabelle 12.3 und Abbildung 12.6.

Tabelle 12.3: ROPE für Modell m_bringtnixtin

Parameter	CI	ROPE_low	ROPE_high	ROPE_Percentage	Effects	Component
(Intercept)	0.95	-0.13	0.13	0.29	fixed	conditional
g	0.95	-0.13	0.13	0.03	fixed	conditional

Tabelle 12.3 zeigt uns, dass 3% des 95%-HDIs im ROPE-Bereich liegt. Das ist nicht viel; aber streng genommen heißt das als Fazit:

Wir können nicht ausschließen, dass der Effekt von g ein praktisch unbedeutsamen Wert hat, also sehr klein und nahe der Null ist. Diese Wahrscheinlichkeit ist allerdings nicht hoch. Es ist somit keine klare Entscheidung möglich.

Ist man sich nicht sicher, wie der ROPE-Wert zu interpretieren ist, kann man auch R fragen:

interpret_rope(0.03)
## [1] "undecided"
## (Rules: default)

Das gleiche Ergebnis zeigt uns anschaulicher Abbildung 12.6.

rope(m_bringtnixtin) %>% plot()

Abbildung 12.6: ROPE für Modell `m_bringtnixtin`

scale_fill_okabeito() ist eine Funktion aus dem Metapaket easystats.³ Das Farbschema nach Okabe und Ito ist gut geeignet, um nominal skalierte Farben zu kodieren (s. Details hier).

Da sich das 95%-CI mit dem ROPE überlappt, kann die Nullhypothese bzw. das ROPE (kein praktisch bedeutsamer Effekt) nicht ausgeschlossen werden.

Eine vergleichbare Information bietet uns die Kennzahl pd, s. Tabelle 13.5. Der Wert für g liegt bei ca. 0.97.

Hinweis

pd gibt die Wahrscheinlichkeit (laut Modell) an, dass der Effekt in der Population negativ bzw. positiv ist (d.h. gleich dem Vorzeichen des Punktschätzers; in diesem Fall negativ). $◻$

Das Modell ist sicher ziemlich sicher, dass der Effekt von g (in der Population) negativ ist. Aber eine kleine Chance, dass der Effekt von g doch (ungefähr) Null oder sogar positiv ist, bleibt.

👨‍🏫 Frau Professor Lustig, oh je! Unser Wirkstoff Bringtnixtin bringt anscheinend gar nix!

👩‍🏫 Herr Professor Sauer, wir müssen erst einmal in Ruhe die Studie replizieren. Eine Schwalbe macht noch keinen Frühling.

Beispiel 12.1 (Hat die Zylinderzahl einen Praktisch-Null-Effekt auf den Spritverbrauch?) Abbildung 12.7 illustriert ein Rope für die Forschungsfrage “Hat die Zylinderzahl einen Praktisch-Null-Effekt auf den Spritverbrauch”. Anders formuliert “Ist der Effekt der Zylinderzahl (auf den Spritverbrauch) vernachlässigbar klein?” Genauer gesagt ist die Posteriori-Verteilung für den (Regressions-)Effekt, $β$ , des Parameters cyl gezeigt (Datensatz mtcars). Wie man sieht, ist die Posteriori-Verteilung (roter Bereich; glockenförmige Verteilung) komplett außerhalb des Bereichs “sehr kleiner” Werte (ROPE; blaues Rechteck rechts). Wir resümieren: “Es ist auszuschließen, dass der Effekt der Variable Zylinder auf den Spritverbrauch praktisch Null (sehr klein) ist”. $◻$

## 
## SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
## Chain 1: 
## Chain 1: Gradient evaluation took 2.3e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.23 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1: 
## Chain 1: 
## Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 1: 
## Chain 1:  Elapsed Time: 0.052 seconds (Warm-up)
## Chain 1:                0.048 seconds (Sampling)
## Chain 1:                0.1 seconds (Total)
## Chain 1: 
## 
## SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
## Chain 2: 
## Chain 2: Gradient evaluation took 1.6e-05 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.16 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2: 
## Chain 2: 
## Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 2: 
## Chain 2:  Elapsed Time: 0.057 seconds (Warm-up)
## Chain 2:                0.052 seconds (Sampling)
## Chain 2:                0.109 seconds (Total)
## Chain 2: 
## 
## SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
## Chain 3: 
## Chain 3: Gradient evaluation took 1.7e-05 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.17 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3: 
## Chain 3: 
## Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 3: 
## Chain 3:  Elapsed Time: 0.056 seconds (Warm-up)
## Chain 3:                0.049 seconds (Sampling)
## Chain 3:                0.105 seconds (Total)
## Chain 3: 
## 
## SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
## Chain 4: 
## Chain 4: Gradient evaluation took 2e-05 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.2 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4: 
## Chain 4: 
## Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 4: 
## Chain 4:  Elapsed Time: 0.056 seconds (Warm-up)
## Chain 4:                0.048 seconds (Sampling)
## Chain 4:                0.104 seconds (Total)
## Chain 4:

Abbildung 12.7: ROPE (blauer Balken) und 95%-KI (roter Bereich) überlappen sich nicht: Die ROPE-Hypothese wird verworfen.

Wenn man die Null bzw. den Nullbereich (ROPE) eines Parameters ausschließt, nennt man das Ergebnis bzw. den Effekt auch “signifikant” (leider ein häufig missbrauchter und missverstandener Begriff). Unser Effekt in diesem Beispiel ist also signifikant (nach dieser Definition). Besser ist es aber, wenn Sie den Begriff vermeiden, und stattdessen davon sprechen, dass Sie einen Effekt gefunden haben (oder nicht oder dass eine unklare Ergebnislage vorliegt). Haben Sie einen Effekt gefunden, so heißt das synonym, dass die Nullhypothese ausgeschlossen ist (falsifiziert ist), natürlich immer auf Basis des vorliegenden Modells bzw. der vorliegenden Daten.

12.2.3.3 Modellgüte

Berechnen wir abschließend noch eine standardisierte Effektstärke der Modellgüte, $R ²$ .

r2(m_bringtnixtin)
## # Bayesian R2 with Compatibility Interval
## 
##   Conditional R2: 0.089 (95% CI [1.838e-07, 0.244])

Also etwa 9% erklärte Varianz. Aber ist das viel oder wenig? Fragen wir Herr Cohen, der hat sich dazu mal Gedanken gemacht.

interpret_r2(.09)
## [1] "weak"
## (Rules: cohen1988)

Nach dieser Einschätzung ist der Effekt von g also schwach.

12.3 Vorher-Nachher-Messung, 1 between-Variable

12.3.1 Design

Sauer & Lustig (2023) fiel auf, dass es sinnvoller ist, zuerst die AV mittels eines Vortests zu messen, dann die Intervention anzuwenden, und dann nachher (Posttest) die AV wieder zu messen. Daher haben sie sowohl vor der Intervention (t1) als auch nach der Intervention (Gabe von Bringtnixtin), t2, die AV (y, Behaltensleistung) gemessen.

Hinweis

Eine Vorher-Nachher-Messung hat den Verteil, dass sie - im Gegensatz zur Nur-Nachher-Messung - unterschiedliche Ausgangswerte in der AV herausrechnet. Damit kommt man oft zu belastbareren, also besseren, Ergebnissen. Bei großen Gruppen wird sich bei einer randomisierten Zuweisung zu den Gruppen der Ausgangswert der AV angleichen. Bei nicht so großen Gruppen kann aber auch bei Randomisierung ein - mitunter erheblicher - Unterschied zwischen den Gruppen verbleiben. Findet man bei der Post-Messung einen Effekt, so kann es sein, dass dieser nicht auf die Intervention beruht, sondern auf die von vornherein vorhandenen Unterschieden zwischen den Gruppen. $◻$

Vergleicht man die Delta-Werte zwischen zwei Gruppen, berechnet man die Differenz zwischen den Gruppen der Delta-Werte. Man spricht daher von einer Difference-in-Difference-Analyse. $◻$

Abbildung 12.8 zeigt den Ablaufplan dieses Experiments.

Abbildung 12.8: Ablaufdiagramm der Bringtnixtin-Studie

DAG des Experiments ist in Abbildung 12.9 dargestellt.

Abbildung 12.9: DAG für der Bringtnixtin-Studie

12.3.2 Deskriptive Analyse

Eine einfache (und sinnvolle) Art, solche Studiendesigns auszuwerten ist die Bildung einer Differenz-Variable⁴. Diese Differenzvariable gibt die Veränderung der fluiden Intelligenz durch die Intervention an. Anders gesagt: Die Differenz ist die IQ-Wert einer Person nach der Intervention minus dem IQ-Wert vor der Intervention: $d = y_{2} - y_{1}$ :

d_bringtnixtin <-
  d_bringtnixtin %>% 
  mutate(d = y2 - y1)

Schauen wir uns die ersten paar d-Werte für jede der beiden Gruppen (g=0 bzw. g=1) an:

id	g	y1	y2	d
1	0	1.37	1.41	0.04
2	0	-0.56	-0.64	-0.07
3	0	0.36	0.51	0.15
21	1	-0.31	-0.71	-0.41
22	1	-1.78	-2.08	-0.30
23	1	-0.17	-0.39	-0.22

Vielleicht ist es anschaulicher, wenn wir die Gruppe 0 in den Text Kontrollgruppe umbenennen und 1 in Experimentalgruppe:

d_bringtnixtin <-
  d_bringtnixtin %>% 
  mutate(g_text =
           case_when(g == 0 ~ "Kontrollgruppe",
                     g == 1 ~ "Experimentalgruppe"))

Hier sind die Mittelwerte für jede der beiden Gruppen:

d_bringtnixtin %>% 
  group_by(g_text) %>%
  summarise(d = mean(d))

Mittelwerte der Veränderung der Behaltensleistung nach Gruppe
g_text	d
Experimentalgruppe	-0.30
Kontrollgruppe	-1.82e-04

Die deskriptiven Kennwerte sind in Abbildung 12.10 dargestellt.

ggbetweenstats(
  data = d_bringtnixtin,
  x = g_text,
  y = d,
  results.subtitle = FALSE  # keine Statistiken zeigen
)

Abbildung 12.10: Veränderung der fluiden Intelligenz (d) in Abhängigkeit der Gruppe; g=0: Kontrollgruppe (Placebo), g=1: Experimentalgruppe (hohe Dosis)

12.3.3 Modellierung und Inferenz

Wir modellieren (in m_bringtnixtin2) jetzt die Veränderung d = y2 - y1 als AV; UV ist wieder g, s. Tabelle 12.4.

m_bringtnixtin2 <- stan_glm(d ~ g,
                            data = d_bringtnixtin)
parameters(m_bringtnixtin2)

Tabelle 12.4: Parameter von m_bringtnixtin2

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	-1.34e-03	(-0.08, 0.08)	51.42%	1.000	3934.00	Normal (-0.15 +- 0.59)
g	-0.30	(-0.41, -0.18)	100%	0.999	4181.00	Normal (0.00 +- 1.17)

Abbildung 12.11 zeigt die Parameterwerte für m_bringtnixtin2,

Abbildung 12.11: Parameterwerte von m_bringtnixtin2 (Intercept ist nicht dargestellt), 95%-ETI; die Null ist nicht enthalten, der Mittelwert ist negativ. ROPE ist als blaues Balken eingezeichnet. Wir können die exakte und die praktische Nullhypothese ausschließen.

Wie man den Parameterwerten entnehmen kann, ist sich das Modell sehr sicher, dass der Effekt von Bringtnixtin negativ ist.

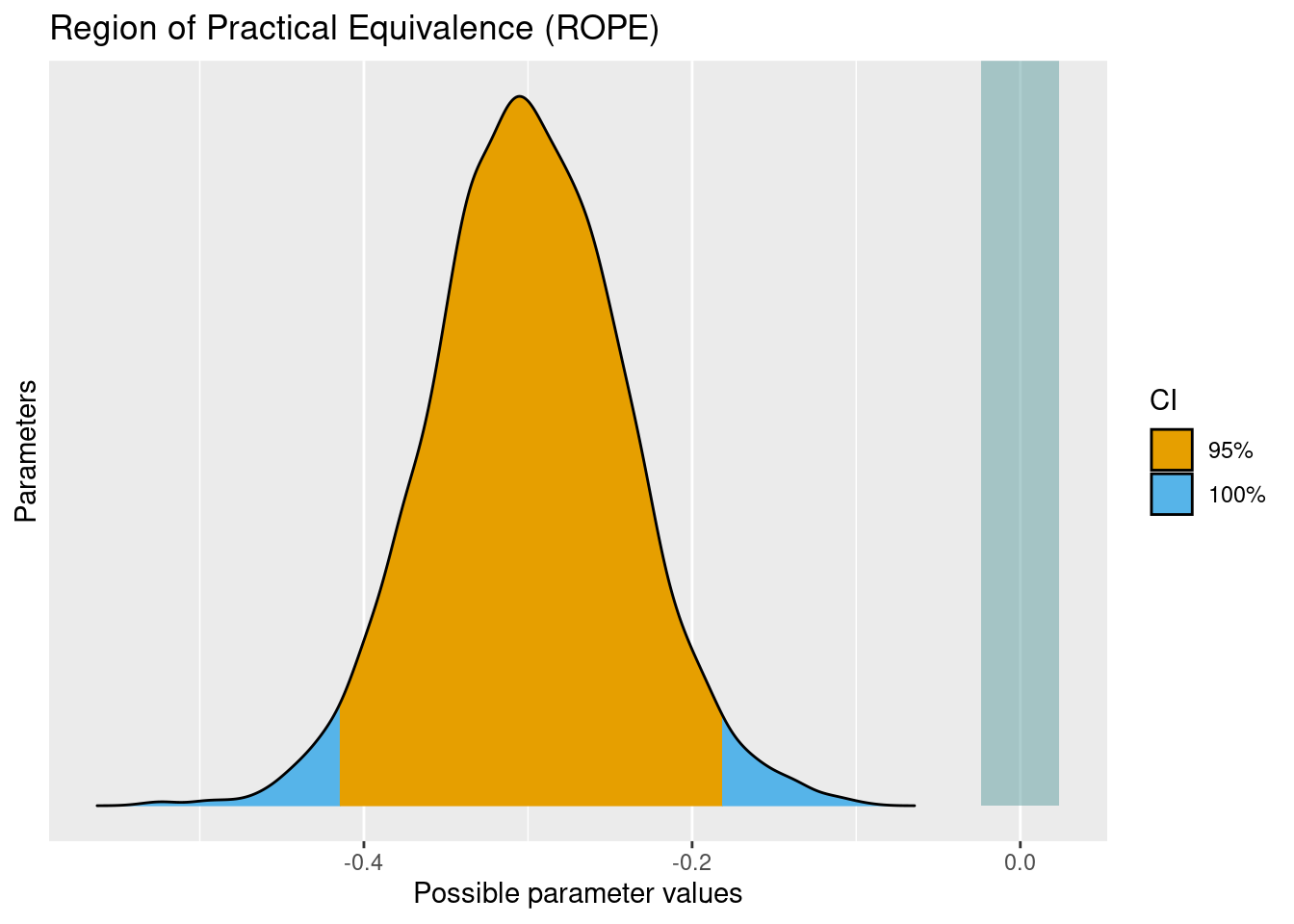
Testen wir noch die Praktisch-Null-Hypothese (für den Effekt von g auf d) mit dem ROPE-Verfahren:

rope(m_bringtnixtin2)

ABCDEFGHIJ0123456789

	Parameter <chr>	CI <dbl>	ROPE_low <dbl>	ROPE_high <dbl>	ROPE_Percentage <dbl>	Effects <chr>
1	(Intercept)	0.95	-0.02377655	0.02377655	0.4565789	fixed
2	g	0.95	-0.02377655	0.02377655	0.0000000	fixed

Das Ergebnis zeigt uns, dass wir die Praktisch-Null-Hypothese ausschließen können: Null Prozent des 95%-HDI liegt im ROPE.

plot(rope(m_bringtnixtin2)) + scale_fill_okabeito()

Abbildung 12.12: 95%-HDI und ROPE überlappt nicht: Wir verwerfen die ROPE Hypothese

12.4 Fallstudie

Hier ist eine Fallstudie einer studentischen Arbeit vorgestellt, in der Einsamkeit experimentell induziert wird und dann der Effekt auf wahrgenommene Einsamkeit untersucht wird (unter anderem).

12.5 Beobachtungsstudien

Gängige Forschungsfragen für Beobachtungsstudien sind im Skript Start:Byes aufgeführt, schauen Sie mal [hier]https://start-bayes.netlify.app/1000-metrische-av).

12.6 1 within-Variable

Eine Studie mit Vorher-Nachher-Messung setzt ein Within-Design um.

Beispiel 12.2 (Statisches Diagramm vs. animiertes Diagramm) Ein Forschungsteam untersuch den Effekt der UV Visualisierungsart V (mit den zwei Stufen V.1 animiert und V.2 statisch) auf die Behaltensleistung (y) von Probanden. Nach jeder Bedingung wird die Behaltensleistung gemessen (anhand von 10 Wissensfragen, die jeweils als “richtig” oder “falsch” bewertet wurden), mit y1 nach V.1 und y2 für V.2. $◻$

12.6.1 Design

Forschungsfrage:

Hat die Diagrammart einen Einfluss auf die Behaltensleistung? Anders gesagt: Unterscheiden sich die Diagrammarten in ihrem Einfluss auf die mittlere Behaltensleistung?

Die zugehörige statistische Hypothese kann man so formulieren: $\bar{d} \neq 0$ , wobei $d = y_{1} - y_{2}$ . $d$ misst also den Unterschied der Behaltensleistung von animierten und statischen Diagrammen, wobei positive Werte zugunsten von statischen Diagrammen sprechen.

Die Modellformel lautet: d ~ 1, das ist ein Intercept-Modell, also ein Modell ohne Prädiktor. Uns interessiert, ob die Variable d im Mittelwert ungleich Null ist oder positiv (zugunsten statischer Diagramme) oder negativ (Behaltensleistung höher bei animierten Diagrammen).

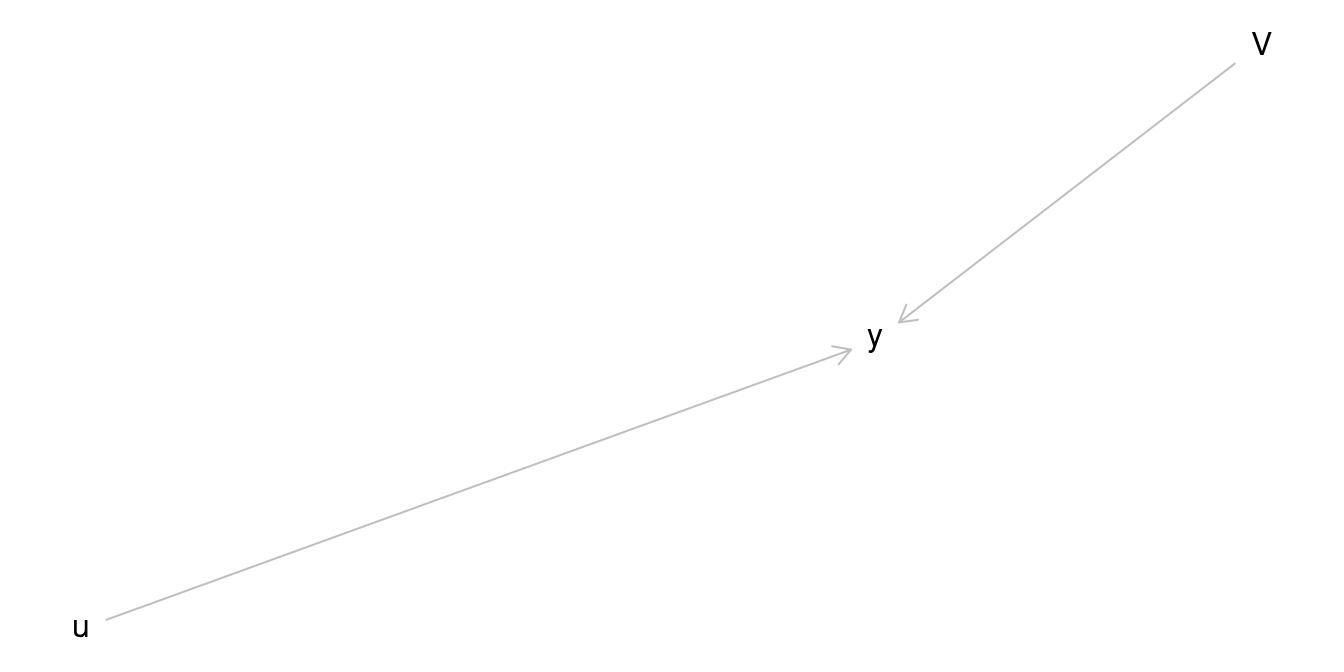
Der Ablauf der Studie (aus Sicht der Probandis) ist in Abbildung 12.13 dargestellt.

Abbildung 12.13: Ablauf der Studie zur Behaltensleistung y2 in Abhängigkeit der Visualisierungsart V (Within-UV mit zwei Stufen, V.1 und V.2). V.1 und V.2 sind jeweils Interventionen und damit Stufen der UV. Alle Versuchspersonen laufen dieselben beiden Interventionen (V.1 und V.2).

Der DAG des Experiments ist in Abbildung 12.14 dargestellt.

Abbildung 12.14: DAG für die Studie zur Behaltensleistung y2 in Abhängigkeit des Visualiserungstyp V

12.6.2 Deskriptive Analyse

Hier sind einige Spieldaten:

d_within <- 
  read_csv("https://raw.githubusercontent.com/sebastiansauer/Lehre/main/data/withindesign.csv") %>% 
  select(-c(y3, g)) # diese beiden Variablen ignorieren wir für den Augenblick

head(d_within)

ABCDEFGHIJ0123456789

id <dbl>	y1 <dbl>	y2 <dbl>
1	7	8
2	7	7
3	4	9
4	7	4
5	6	7
6	5	4

Wir berechnen d, was die zentrale Variable der Forschungsfrage ist.

d_within <-
  d_within %>% 
  mutate(d = y1 - y2)

head(d_within)

ABCDEFGHIJ0123456789

id <dbl>	y1 <dbl>	y2 <dbl>	d <dbl>
1	7	8	-1
2	7	7	0
3	4	9	-5
4	7	4	3
5	6	7	-1
6	5	4	1

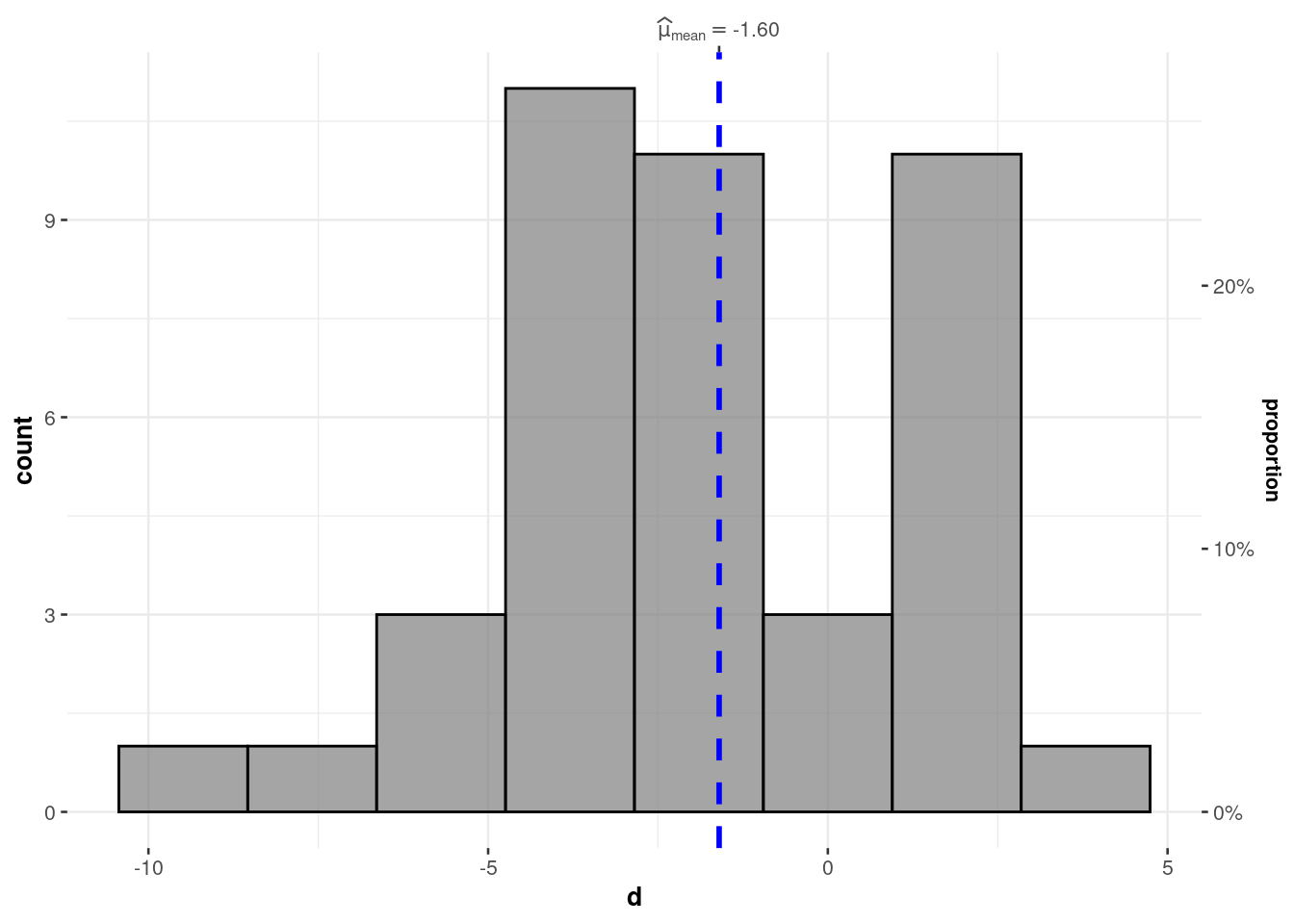
Es klingt trivial, aber man muss sich ein Bild von den Daten (hier d) machen, wortwörtlich, s. Abbildung 12.15.

gghistostats(d_within,
             x = d,
             results.subtitle = FALSE  # verzichte auf zusätzliche Statistiken
             )

Abbildung 12.15: Die Verteilung von d: Die Behaltensleistung ist im Mittel besser für animierte Diagramme (in diesen Daten)

Da d im Mittel negativ ist, ist der Mittelwert von y2 (animiert) höher als der von y1 (statisch).

Lassen wir uns die deskriptiven Kennwerte ausgeben, s. Tabelle 12.5.

d_within %>% 
  describe_distribution(d)

Tabelle 12.5: Statistiken für d

Variable	Mean	SD	IQR	Range	Skewness	Kurtosis	n	n_Missing
d	-1.60	2.63	4	(-9.00, 3.00)	-0.55	0.30	40	0

Um die Daten noch anders visualisieren zu können, formen wir sie ins “lange Format” um.

d_long <-
  d_within %>% 
  pivot_longer(cols = c(y1, y2), names_to = "time", values_to = "y")

Hier ist ein Auszug aus der Tabelle:

head(d_long)

ABCDEFGHIJ0123456789

id <dbl>	d <dbl>	time <chr>	y <dbl>
1	-1	y1	7
1	-1	y2	8
2	0	y1	7
2	0	y2	7
3	-5	y1	4
3	-5	y2	9

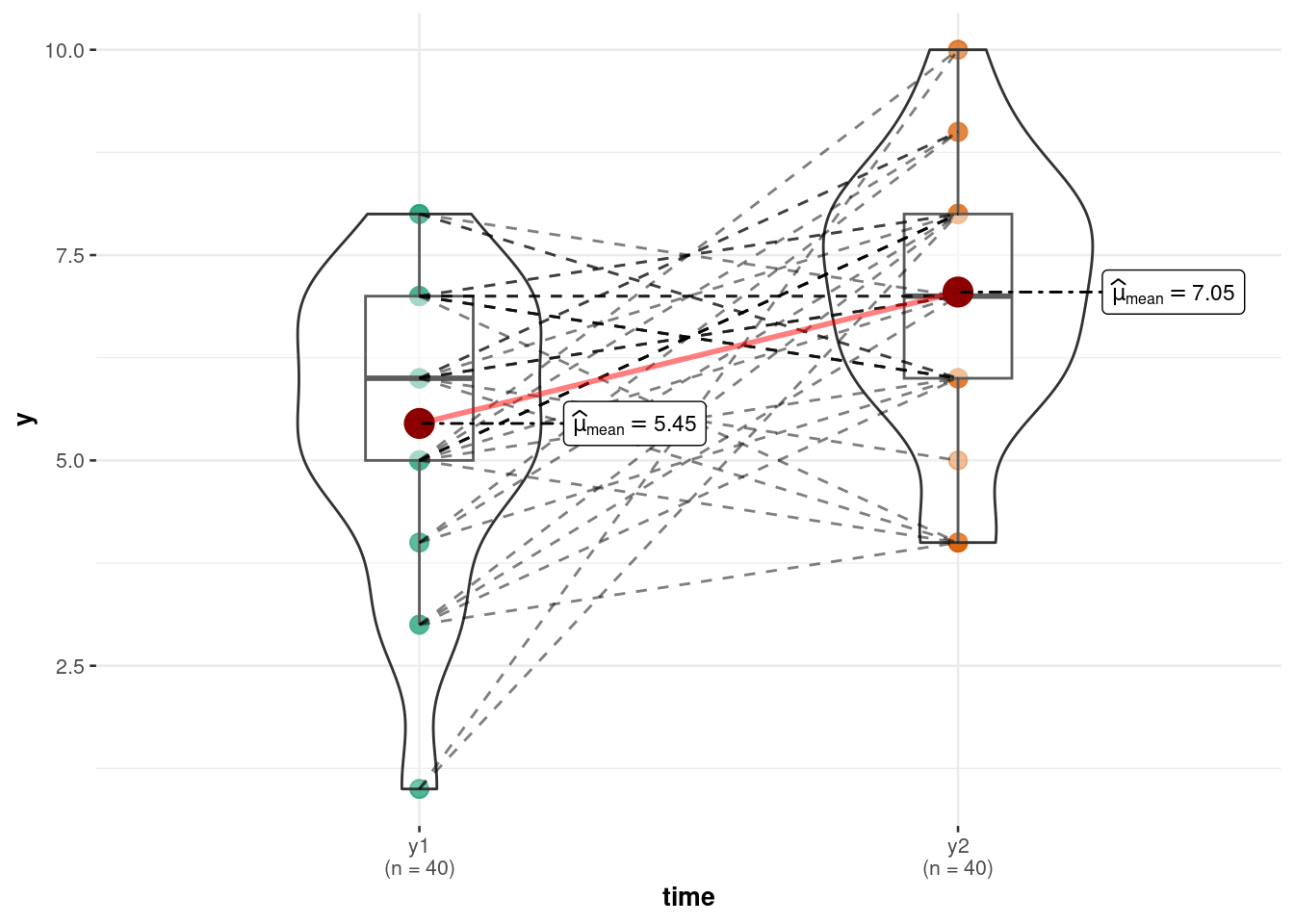
Visualisieren wir uns die Daten, s. Abbildung 12.16.

ggwithinstats(
  data = d_long,
  x = time,
  y = y,
  results.subtitle = FALSE  # verzichte auf zusätzliche Statistiken
)

Abbildung 12.16: Der Unterschied in der Behaltensleistung pro Versuchsperson; im Durchschnitt ist der Wert bei y2 höher als bei y1

12.6.3 Modellierung und Inferenz

Wir berechnen das Modell (m_within), s. Tabelle 12.6:

m_within <- stan_glm(d ~ 1, 
                     data = d_within)
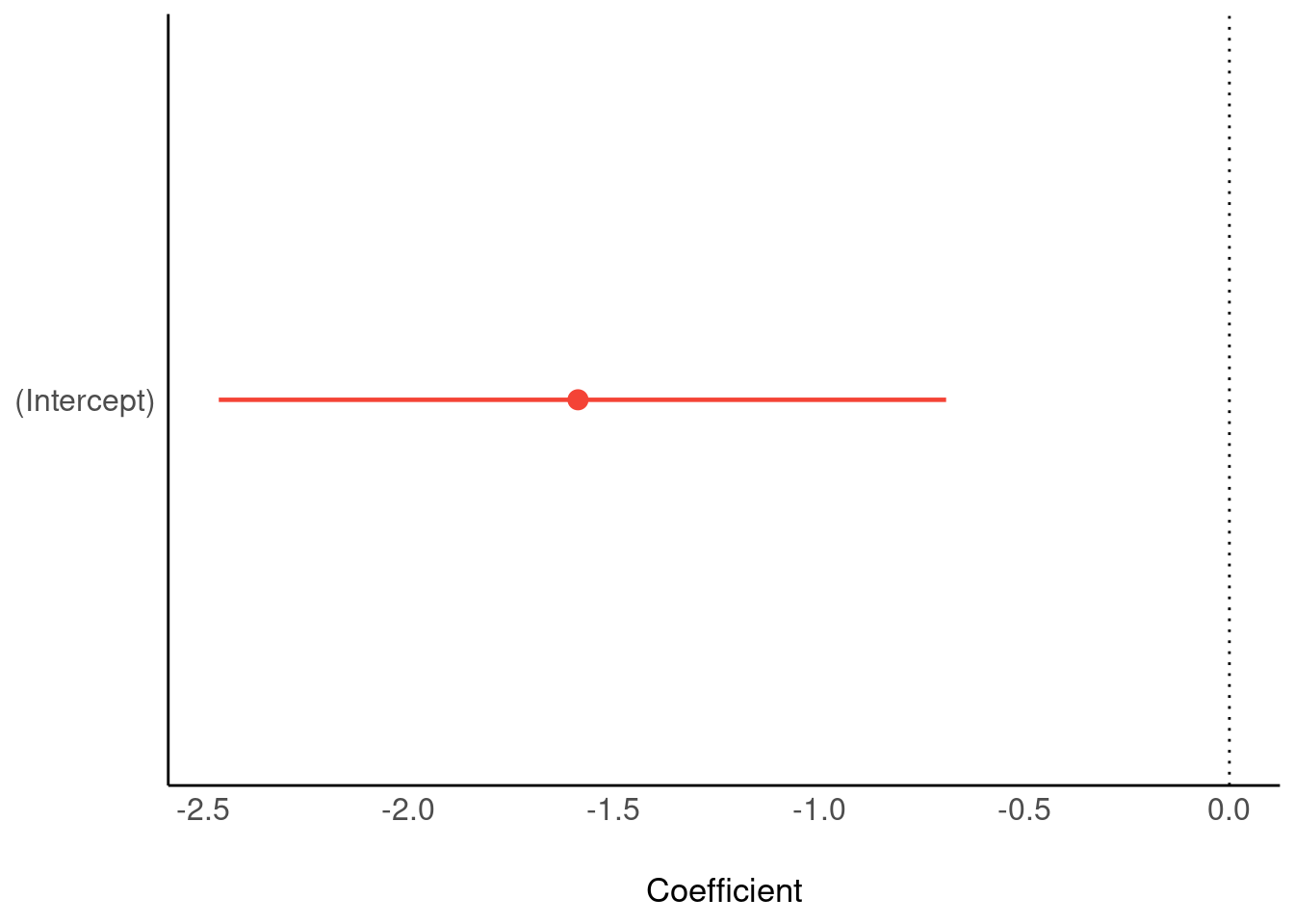
parameters(m_within)

Tabelle 12.6: Modellparameter von m_within

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	-1.59	(-2.46, -0.69)	100%	1.000	2536.00	Normal (-1.60 +- 6.57)

Hier ist eine Visualisierung des 95%-ETI des Unterschieds (d) zwischen den beiden Bedingungen (Abbildung 12.17).

parameters(m_within) %>% plot(show_intercept = TRUE)

Abbildung 12.17: 95%-CI für d (Achsenabschnitt mit Modell m_within)

Hinweis

Wenn Sie die parameters plotten und nur einen Intercept haben, müssen Sie mit show_intercept=TRUE einschalten, dass er gezeigt wird. Sonst gibt es eine Fehlermeldung. $◻$

Wie man sieht, ist die Null nicht im CI enthalten. Wir können daher resümieren, dass es einen Unterschied zwischen den Bedingungen (statisch vs. animiert) gibt hinsichtlich y2 (Behaltensleistung). Die Behaltensleistung animierter Diagramme ist der von statischen Diagrammen überlegen (laut diesem Modell). Die exakte Nullhypothese ist zu verwerfen. Natürlich könnte man jetzt noch ein Rope berechnen.

12.6.4 Vertiefung

In diesem Blog-Post findet eine kleine Fallstudie zur Analyse von “Vorher-Nachher-Daten”.

12.7 1 within-Variable, 1 between-Variable

12.7.1 Design

Forschungsfrage:

Hat die Diagrammart einen Einfluss auf die Behaltensleistung? Anders gesagt: Unterscheiden sich die Diagrammarten in ihrem Einfluss auf die Behaltensleistung? Dabei kontrollieren wir die Reihenfolge.

Forschungspraktisch bedeutet das, dass es zwei (Between-)Gruppen, g1 und g2 in diesem Experiment gibt. Diese beiden Gruppen definieren eine Between-UV, G, die die Reihenfolge der Darbietung kontrolliert, s. Abbildung 12.18. Die Diagrammart V ist auch eine UV, aber als Within-UV konzipiert (mit den zwei Stufen V.1 und V.2).

Abbildung 12.18: Ablaufdiagramm für die Studie mit der Modellgleichung mit einer Within-UV (V) und einer Between-UV (g)

Da es zwei UVs gibt, gibt es auch zwei Hypothesen:

H1: $\bar{d} < 0$ , mit $d = y_{1} - y_{2}$ : Die mittlere Behaltensleistung ist in der Bedingung animiert höher als in der Bedingung statisch.
H2: ${\bar{d}}_{g .1} = {\bar{d}}_{g .2}$ : Der Unterschied in der Behaltensleistung zwischen den zwei Bedingung unterscheidet sich nicht von der Reihenfolge der Darbietung.

Die Modellformel lautet: y ~ 1 + g. Das kann man synonym so schreiben: y ~ g. Dabei meint y meint die Behaltensleistung; statistisch erfassen wir den Effekt auf y anhand des Differenzmaßes d.

Der DAG des Experiments ist in Abbildung 12.19 dargestellt.

Abbildung 12.19: DAG für die Studie mit der Modellgleichung mit einem Within- und einem Between-Faktor. Es wird kein Effekt für g erwartet (daher kein Pfeil von g auf y), wohl aber ein Effekt für V

12.7.2 Deskriptive Analyse

Hier sind einige Spieldaten:

d_within <- 
  read_csv("https://raw.githubusercontent.com/sebastiansauer/Lehre/main/data/withindesign.csv") %>% 
  select(-c(y3)) # die  Variable `y3` ignorieren wir für den Augenblick

head(d_within)

ABCDEFGHIJ0123456789

id <dbl>	y1 <dbl>	y2 <dbl>	g <chr>
1	7	8	A
2	7	7	A
3	4	9	A
4	7	4	A
5	6	7	A
6	5	4	A

Wir berechnen d, der Unterschied zwischen den beiden Bedingungen:

d_within <-
  d_within %>% 
  mutate(d = y1 - y2)

head(d_within)

ABCDEFGHIJ0123456789

id <dbl>	y1 <dbl>	y2 <dbl>	g <chr>	d <dbl>
1	7	8	A	-1
2	7	7	A	0
3	4	9	A	-5
4	7	4	A	3
5	6	7	A	-1
6	5	4	A	1

Betrachten wir den Unterschied von d zwischen den Gruppen (H2), s. Abbildung 12.20.

ggbetweenstats(
  d_within,
  x = g,
  y = d,
  results.subtitle = FALSE
)

Abbildung 12.20: Der Unterschied der Behaltensleistung (d) in Abhängigkeit von der Reihenfolge der Darbietung

Es gibt einen gewissen Unterschied zwischen den beiden Reihenfolgen (A und B) wie Abbildung 12.20 zeigt; die Reihenfolge könnte also einen Einfluss auf d haben. Aber wir müssen inferenzstatistisch prüfen, wie groß der Einfluss ist.

12.7.3 Inferenzanalyse

Berechnen wir m_within2, das nicht nur den Intercept prüft (wie m_within1), sondern auch zusätzlich den Effekt der Reihenfolge (g), vgl. Tabelle 12.7.

m_within2 <- stan_glm(d ~ g, 
                      data = d_within)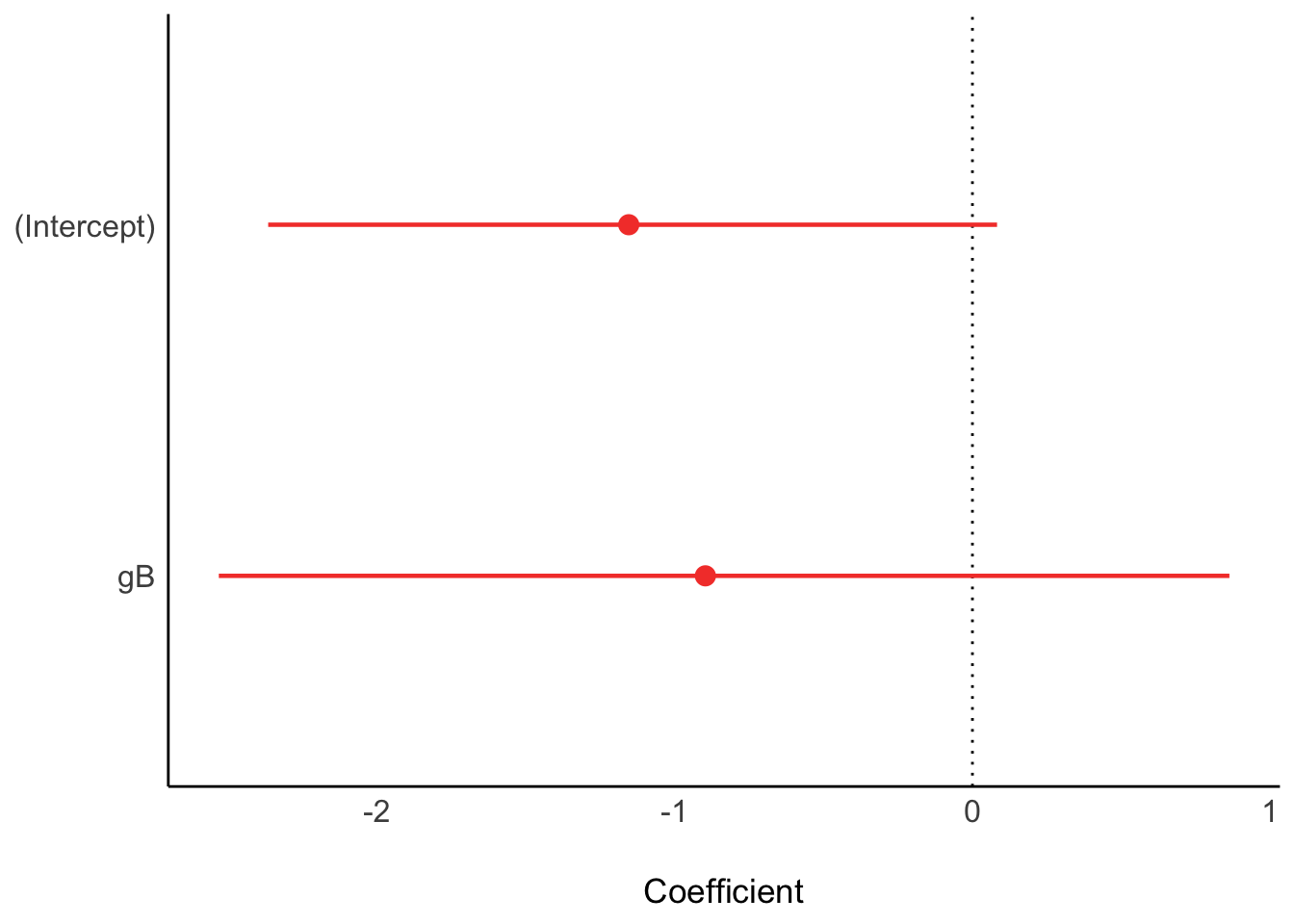

Tabelle 12.7: Modellparameter von m_within2

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	-1.15	(-2.33, -8.72e-03)	97.60%	0.999	3902.00	Normal (-1.60 +- 6.57)
gB	-0.89	(-2.61, 0.73)	86.28%	1.000	3684.00	Normal (0.00 +- 12.98)

Für beide Kennwerte zeigt sich, dass die Null im Schätzbereich enthalten ist. Die Null Hypothese kann also jeweils nicht ausgeschlossen werden. Für H2 wäre es interessant, ob die Nullhypothese bestätigt werden kann; die Ergebnisse sprechen aber dagegen. Insgesamt ist die Befundlage uneindeutig.

Das CI für die Reihenfolge (Variable gB) beinhaltet die Null; Daher kann ein Nulleffekt der Reihenfolge - also kein Effekt der Reihenfolge - nicht ausgeschlossen werden, g=0 ist also im Bereich der plausiblen Werte.

Der Effekt für d ((Intercept)) zeigt ein Intervall, das die Null (knapp) enthält. Daher können wir wir die Nullhypothese nicht mit hoher Sicherheit ausschließen.

In Summe:

H1: (Höhere Behaltensleistung von animiert) konnte nicht bestätigt werden, aber tendenziell fand sich ein Effekt in erwarteter Richtung (zugunsten einer höheren Behaltensleistung von animiert).
H2: (Abwesenheit eines Reihenfolgeeffekts) konnte nicht bestätigt werden; die Ergebnislage war uneindeutig.

12.8 Vertiefung

12.8.1 1 within-Variable mit mehr als zwei Stufen

VERTIEFUNG - Sie können diesen Abschnitt ohne Gefahr ignorieren.

12.8.2 Design

Eine Forscherin hat die Gesundheit (y) von Studentis drei Mal (t1, t2, t3) im Zeitraum eines Semesters untersucht.

Ihre Forschungsfrage lautet, ob sich die Gesundheit im Laufe des Semesters substanziell verändert. Ihre Hypothese lautet, dass die Werte über die Zeit hinweg stabil bleiben.

12.8.3 Deskriptive Analyse

Hier sind einige Spieldaten:

d_within <- 
  read_csv("https://raw.githubusercontent.com/sebastiansauer/Lehre/main/data/withindesign.csv")

head(d_within)

ABCDEFGHIJ0123456789

id <dbl>	y1 <dbl>	y2 <dbl>	y3 <dbl>	g <chr>
1	7	8	9	A
2	7	7	10	A
3	4	9	9	A
4	7	4	9	A
5	6	7	8	A
6	5	4	9	A

Hier benötigen wir die Daten in Langform; wir müssen also vom Breitformat zum Langformat pivotieren:

d_long <-
  d_within %>% 
  pivot_longer(cols = y1:y3, 
               names_to = "time", 
               values_to = "y")

head(d_long)

ABCDEFGHIJ0123456789

id <dbl>	g <chr>	time <chr>	y <dbl>
1	A	y1	7
1	A	y2	8
1	A	y3	9
2	A	y1	7
2	A	y2	7
2	A	y3	10

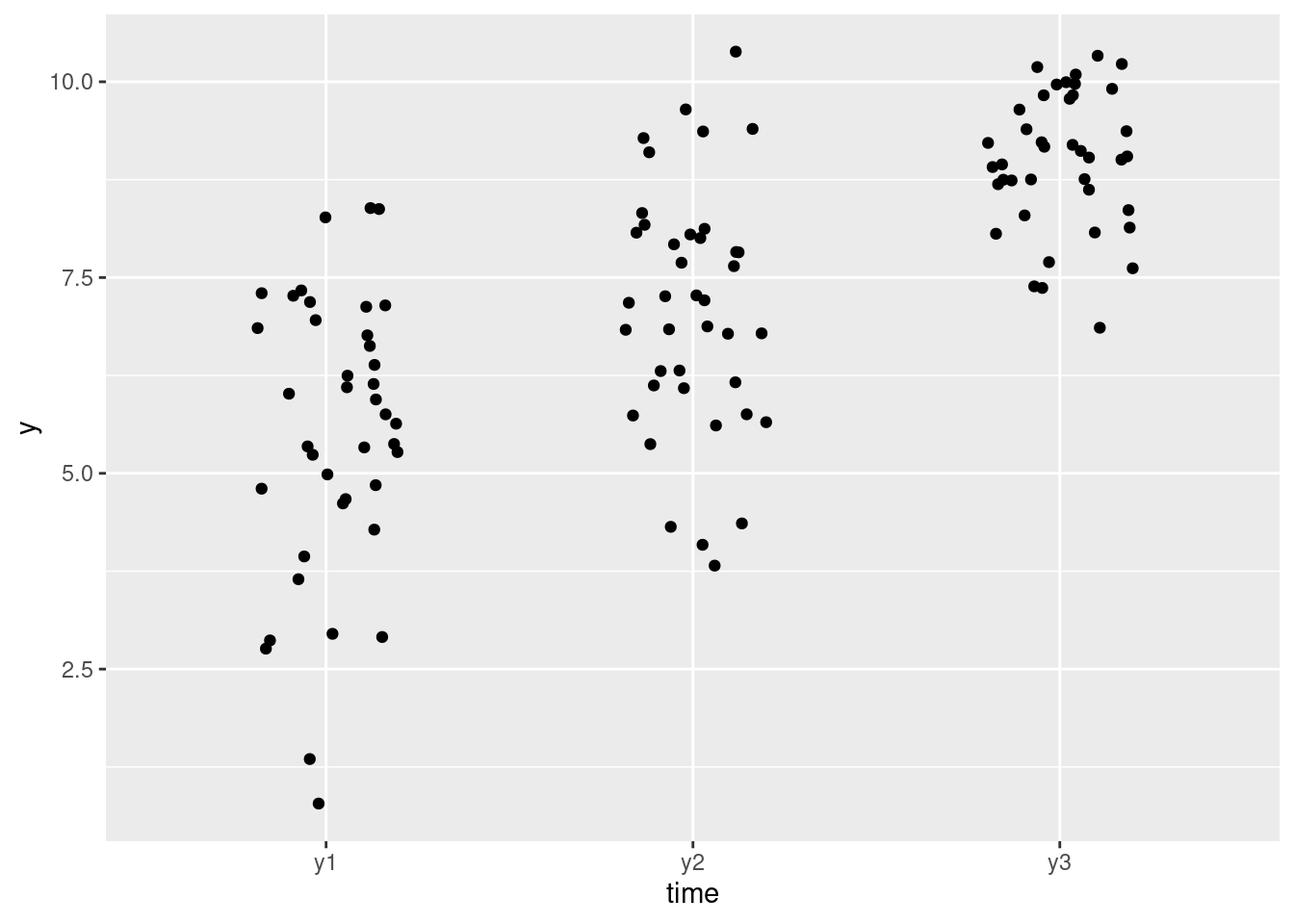
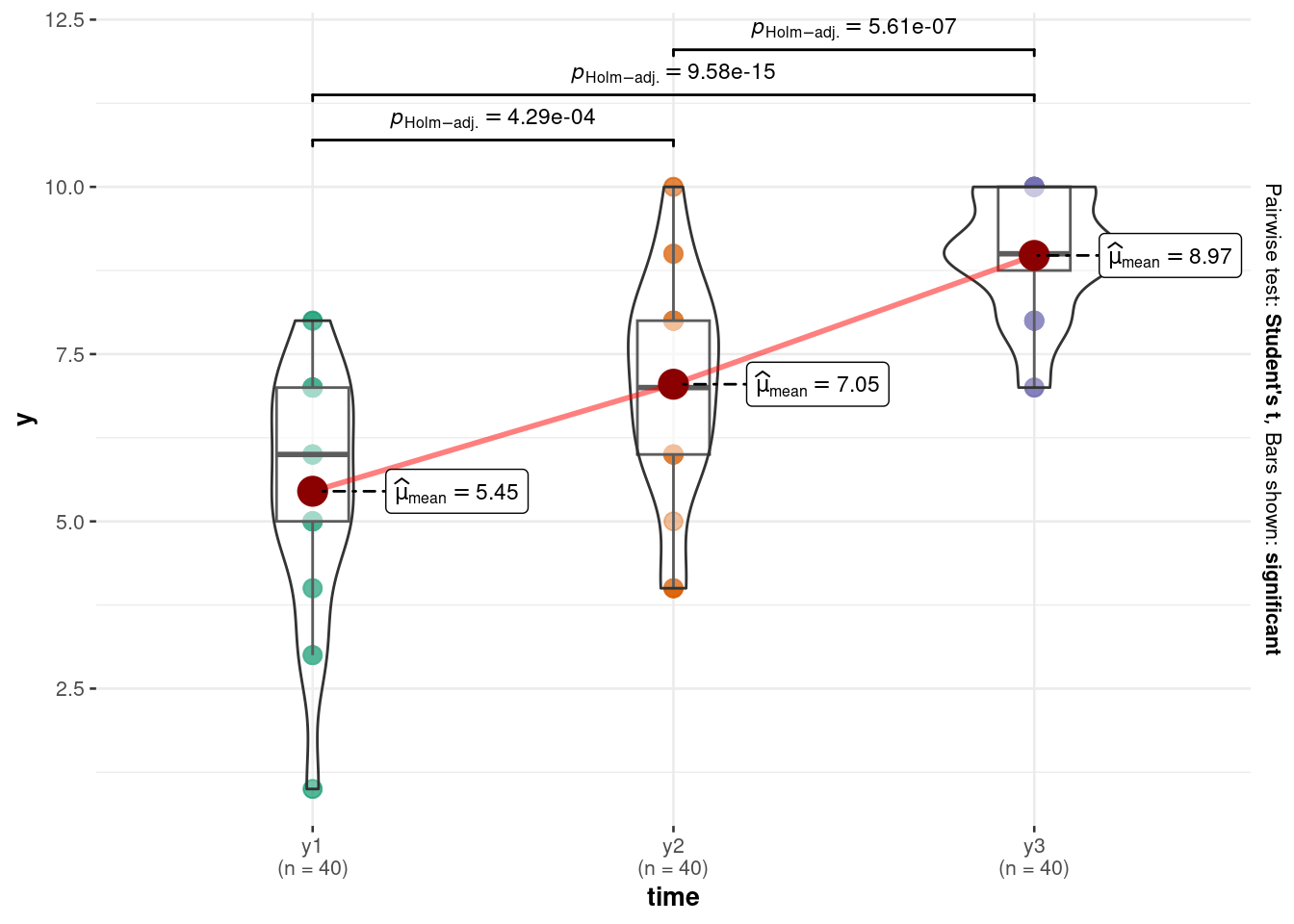
Es hilft (wie meistens), sich die Daten zu visualisieren, s. Abbildung 12.21.

p_y123_a <-
  d_long %>% 
  ggplot(aes(x = time, y = y)) +
  geom_jitter(width = .2)

p_y123_b <-
  ggwithinstats(d_long, 
                x = time,
                y = y,
                results.subtitle = FALSE)

p_y123_a
p_y123_b

Berechnen wir die Mittelwerte von y pro Messzeitpunkte sowie die Veränderung von t1 zu t2 bzw. von t2 zu t3, s. Tabelle 12.8.

d_long %>% 
  group_by(time) %>% 
  summarise(y_mean = mean(y)) %>% 
  mutate(d = y_mean - lag(y_mean))

Tabelle 12.8: Mittelwerte von y pro Messzeitpunkte (y_mean) sowie die Veränderung von t1 zu t2 bzw. von t2 zu t3 (d)

time	y_mean	d
y1	5.45
y2	7.05	1.60
y3	8.97	1.92

12.8.4 Modellierung und Inferenz

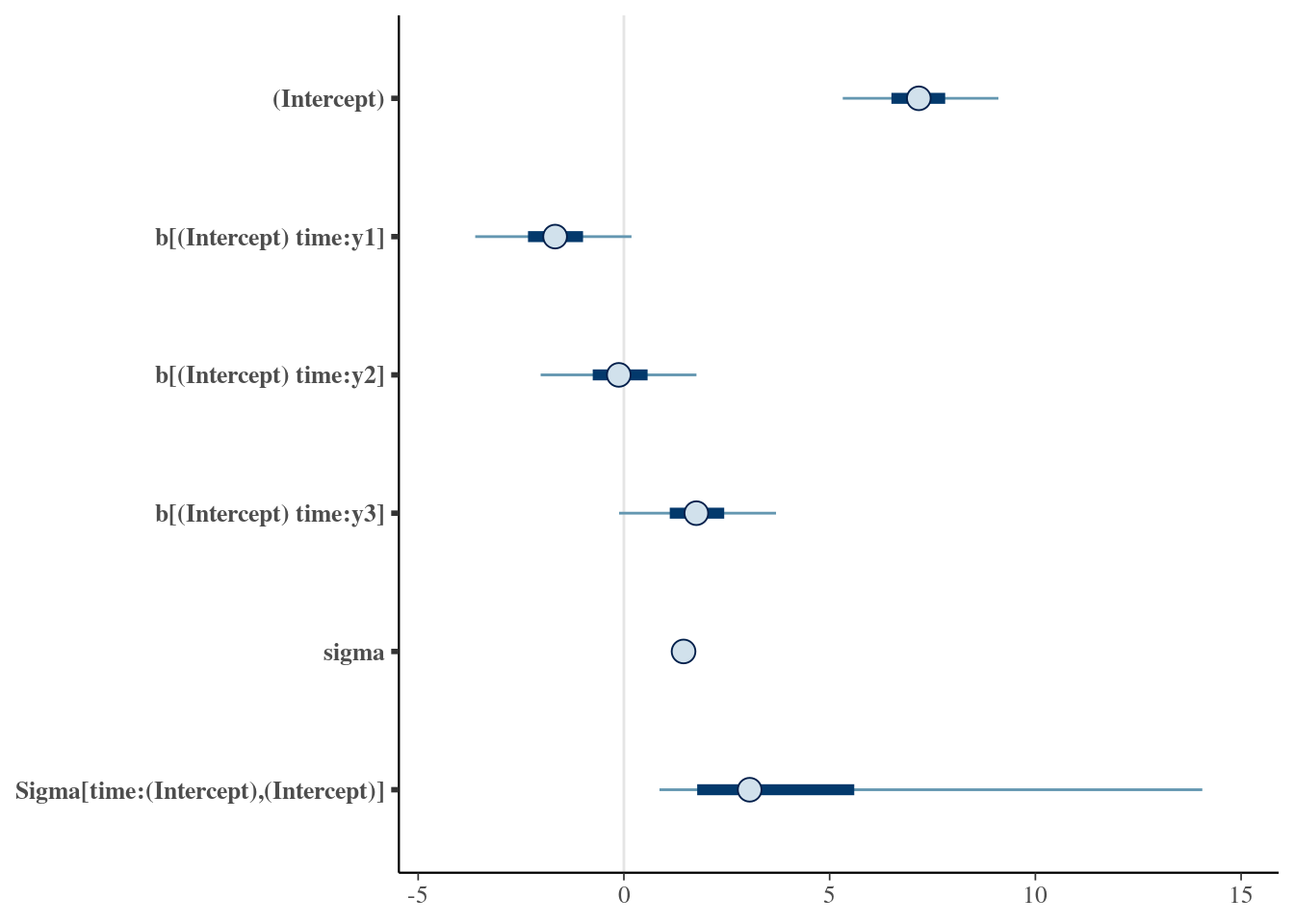
m_within3 <- stan_lmer(y ~ 1 + (1 | time), data = d_long, refresh = 0)
summary(m_within3)
## 
## Model Info:
##  function:     stan_lmer
##  family:       gaussian [identity]
##  formula:      y ~ 1 + (1 | time)
##  algorithm:    sampling
##  sample:       4000 (posterior sample size)
##  priors:       see help('prior_summary')
##  observations: 120
##  groups:       time (3)
## 
## Estimates:
##                                       mean   sd   10%   50%   90%
## (Intercept)                          7.2    1.2  5.8   7.2   8.6 
## b[(Intercept) time:y1]              -1.7    1.2 -3.1  -1.7  -0.3 
## b[(Intercept) time:y2]              -0.1    1.2 -1.5  -0.1   1.2 
## b[(Intercept) time:y3]               1.8    1.2  0.3   1.7   3.2 
## sigma                                1.5    0.1  1.3   1.4   1.6 
## Sigma[time:(Intercept),(Intercept)]  4.8    5.6  1.1   3.1  10.1 
## 
## Fit Diagnostics:
##            mean   sd   10%   50%   90%
## mean_PPD 7.2    0.2  6.9   7.2   7.4  
## 
## The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
## 
## MCMC diagnostics
##                                     mcse Rhat n_eff
## (Intercept)                         0.0  1.0  1089 
## b[(Intercept) time:y1]              0.0  1.0  1112 
## b[(Intercept) time:y2]              0.0  1.0  1115 
## b[(Intercept) time:y3]              0.0  1.0  1124 
## sigma                               0.0  1.0  2784 
## Sigma[time:(Intercept),(Intercept)] 0.2  1.0  1327 
## mean_PPD                            0.0  1.0  4098 
## log-posterior                       0.1  1.0  1331 
## 
## For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Die Schreibweise (1 | time) soll sagen, dass die Messwerte innerhalb von time verschachtelt sind und variieren. Die 1 sagt, dass es sich bei der variierenden Größe um den Intercept handelt, nicht um eine UV.

Ein “fixer” Effekt ist ein Effekt, für den kein Pooling stattfindet, das ist hier der Intercept.

Nur die festen (fixed) Effekte kann man sich so ausgeben lassen:

fixef(m_within3)
## (Intercept) 
##    7.189574

Im Durchschnitt werden ca. 7.1 Fragen richtig beantwortet (Gesamtmittel); das ist die Information die der Punktschätzer des Intercepts bietet.

Nur die Random-Effekte kann man sich so ausgeben lassen:

ranef(m_within3)
## $time
##    (Intercept)
## y1  -1.6846244
## y2  -0.1179905
## y3   1.7274384
## 
## with conditional variances for "time"

Das sind jeweils die Abweichungen der Gruppenmittelwerte (y1, y2, y3) vom Gesamtmittel. Die Random-Effekte kann man sich visualisieren lassen, s. Abbildung 12.22.

plot(m_within3)

Abbildung 12.22: 95%-CI der Random-Effekte von `m_within3`

12.8.5 Mediatoranalyse

Hier findet sich eine Einführung in die Mediationsanalyse. Dieses R-Paket stellt ebenfalls komfortable Funktionen zur Verfügung für Mediationsanalysen.

12.9 Fazit

Unter Modellieren versteht man in der Forschungspraxis meist ein Regressionsmodell der Form av ~ uv. Die Inferenzstatistik hilft, die Modellparameter mit Schätzwerten für die Population zu versehen.

12.10 Aufgaben

Schauen Sie sich im Datenwerk die Aufgaben mit folgenden Tags an: