10 Auswerten: Grundlagen
Versuchsplanung, Statistik, R, Datenanalyse, Psychologie, Forschung
10.1 Lernsteuerung
10.1.1 Lernziele
- Sie können die typischen Schritte einer Datenanalyse (von Forschungsdaten z. B. aus der Psychologie) benennen.
- Sie können den Unterschied zwischen Deskriptiv- und Inferenzstatistik benennen.
- Sie können die Relevanz von Reproduzierbarkeit erläutern.
10.1.2 Position im Lernpfad
Sie befinden sich im Abschnitt “Auswertung” in Abbildung 1.2. Behalten Sie Ihren Fortschritt im Projektplan im Blick, s. Abbildung 1.3.
10.1.3 Benötigte R-Pakete und Daten
In diesem Kapitel benötigen Sie die folgenden R-Pakete:
Wir arbeiten mit dem Datensatz extra, aus dem Paket pradadata. in dem Datensatz werden Korrelate zum Persönlichkeitsmerkmal Extraversion untersucht. Ein Codebook findet sich hier.
data_url <- "https://raw.githubusercontent.com/sebastiansauer/modar/master/datasets/extra.csv"
extra <- data_read(data_url) # aus `{easystats}`Anstelle der Funktion data_read könnten Sie auch read_csv (Tidyverse) oder read.csv (Standard-R) verwenden.
10.2 Überblick zur Datenanalyse
Mühsam haben Sie Ihre Studie geplant, minutiös den Versuchsplan ausgeheckt, pedantisch die Messinstrumente bestimmt. Dann! Die Datenerhebung! Versuchspersonen, manche nervig, manche freundlich. Ist Forschung denn so anstrengend? Endlich! Geschafft – die Daten sind im Sack, sozusagen. Die Datenerhebung ist abgeschlossen. Was jetzt?
10.2.1 Wozu ist das gut?
Würden Sie einem Medikament trauen, von dem es heißt, das Forschungsteam hatten keinen Bock, Statistik ist zu stressig, aber die Typen aus dem Forschungsteam hätten da so ein Gefühl, könnte schon was bringen, die Pille, immer rein damit. Was?! Sie zögern sich das Medikament einzuwerfen? Sie wüssten es lieber genauer, sicherer, belastbarer? Es ginge schließlich um ihre Gesundheit?
Also gut, Sie haben es so gewollt: Gehen Sie geradeaus weiter zur Statistik.
10.2.2 Über 7 Brücken musst du gehen: Die Schritte der Datenanalyse
Abbildung 10.1 stellt die typischen Schritte (“Brücken”) der Datenanalyse dar.
In etwas mehr Detail sieht der Fortgang Ihrer Datenanalyse so aus:
Einlesen und Aufbereiten: Nachdem Sie die Daten in R importiert haben, bereiten Sie sie auf. Das klingt läppisch, langweilig fast und nicht so cool wie Modellieren. Schon richtig. Fakt ist aber, dass dieser Teil der Analyse häufig ein Großteil der Zeit benötigt. Wahr ist: Das Daten aufbereiten ist enorm wichtig. Typische Beispiele für solche Tätigkeiten sind das Behandeln fehlender Werte, das Umformen von Tabellen und das Zähmen von Extremwerten
Zusammenfassen: Nachdem Sie die in Ordnung gebracht haben, fassen Sie sie zusammen, um zentrale Trends zu verstehen. Praktisch gesprochen berechnen Sie Maße der Lage, der Streuung und des Zusammenhangs.
Visualisieren: Der Mensch ist halt ein Augentier. So ein schönes Diagramm macht einfach was her und besticht auch den strengsten Gutachter.
Modellieren: Ah, hier kommt der Teil, in dem der Connaisseur seine Muskeln spielen lassen kann: Bayes-Inferenz, multiple Regression, Moderation, Mediation, Kausalanalyse… Ich weiß, Sie können Ihre Freude kaum noch zügeln, aber geduldigen Sie sich noch einen kleinen Augenblick.
Interpretieren: So ein Modell bzw. die entsprechende Funktion in R spuckt einige Zahlen aus. Aber was sagt uns das jetzt? Das würden Sie auch gerne wissen? Prima! Finden wir es zusammen raus.
Kritisieren: Jetzt müssen Sie stark sein. Keine Analyse ist perfekt. Keine Studie ist abschließend. Niemand hat bislang den goldenen Gral gefunden. Okay, aber bisher haben Sie sich auch noch nicht an der Sache versucht! Jedenfalls bricht niemanden ein Zacken aus der Krone, wenn man aufzeigt, wo noch Forschungslücken sind, auch nach der eigenen Studie. Oder sogar, welche Schwächen die eigene Studie bzw. Analyse hat und was man beim nächsten Mal noch besser machen könnte.
Amüsieren: So, irgendwann ist auch gut. Jetzt belohnen Sie sich mal für die ganze harte Arbeit des Studierens.
10.3 Reproduzierbarkeit
Transparenz (vgl. Definition 2.4) ist ein zentrales oder das zentrale Gütemaße der Wissenschaft. Darum sollten Sie alles dran setzen, dass Ihre Studie bzw. die Analyse Ihrer Daten nachvollziehbar ist.
Wesentliche Faktoren für Reproduzierbarkeit sind:
- Sie reichen Ihre Rohdaten ein (inkl. Codebook)
- Sie reichen Ihr Analyseskript ein
- Sie reichen Ihre Stimuli ein (sofern nicht öffentlich verfügbar)
- Sie reichen Ihre Messinstrumente ein (sofern nicht öffentlich verfügbar)
- Sie dokumentieren Ihr Vorgehen und reichen es ein
10.4 Codebook
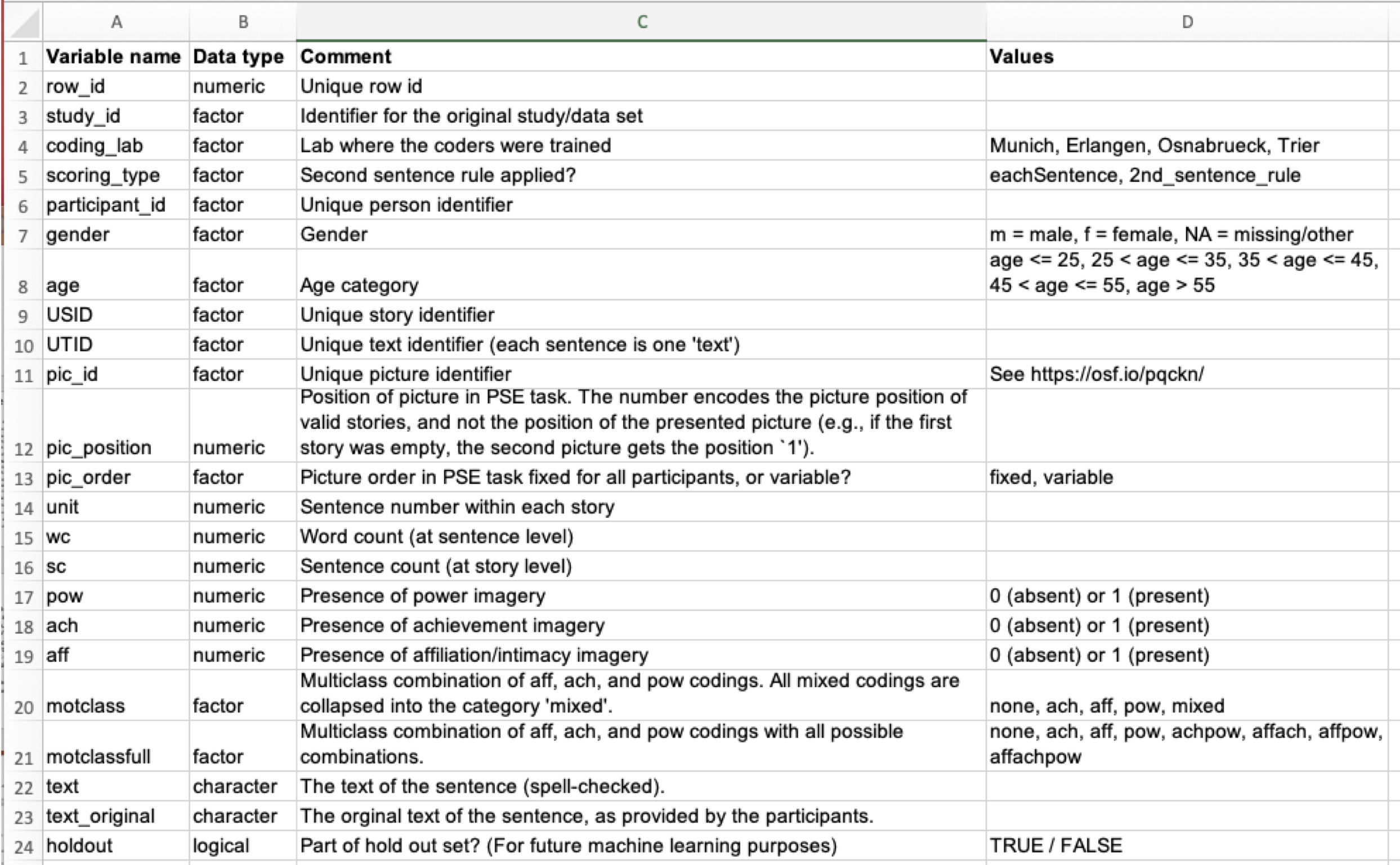
Ein Teil der Dokumentation ist ein Codebook (auch Data-Dictionary genannt). Ein Codebook erläutert die Namen der Variablen in Ihrer (Roh-)Datentabelle, s. Abbildung 10.2.
10.5 Wir brauchen brave Daten
Wie muss eine Tabelle aufgebaut sein, damit man sie gut in R importieren kann, bzw. gut damit weiterarbeiten kann?
Im Überblick sollten Sie auf Folgendes achten:
- Wenn Sie händisch Daten eintragen, hacken Sie das einfach in Excel o.Ä. sein.
- CSV-Dateien bieten sich als Datenformat an.
- Alternativ kann man auch Excel-Dateien in R importieren.
- Es muss genau eine Kopfzeile geben.
- Es darf keine Lücken geben (leere Zeilen oder Spalten oder Zellen).
- Vermeiden Sie Umlaute und Leerzeichen in den Variablennamen.
- Die Daten sollten dem Prinzip von “tidy data” folgen.
Beachten Sie das Prinzip von “tidy data”:
- In jeder Zeile steht eine Beobachtung.
- In jeder Spalte steht eine Variable.
- In jeder Zelle steht eine Wert.
Hier ist eine gute Quelle für weitere Erläuterung zu diesem Thema.
10.6 Ich brauche Hilfe bei der Datenanalyse!
Sie benötigen Hilfe für Ihre Datenanalyse? Hier sind einige Hilfestellungen.
10.6.1 Tipps zum Start
- Setzen Sie die Analysen wie in Kapitel 12 dargestellt um (vgl. QM2), falls Sie das noch nicht gemacht haben.
- Gehen Sie die Checkliste zur Datenanalyse durch, s. Kapitel 10.6.2.
- Schauen Sie sich die Videos auf meinem YouTube-Kanal an, besonders die Playlists aus Kapitel 12.1.4.2.
- Prüfen Sie, ob Ihre (Regressions-)Modelle zu Ihren Hypothesen bzw. Forschungsfragen passen.
- Schauen Sie sich die als empfehlenswert ausgestellten Arbeiten an (s. Moodle) oder Kapitel 14.1.
10.6.2 Checkliste zur Datenanalyse
Hier sehen Sie im Überblick die Schritte, die in vielen Fällen sinnvoll sind, um Daten auf einem guten Niveau auszuwerten.
-
Vorverarbeitung
- Importieren
- Aufbereiten (Umkodieren, fehlende Wert versorgen, Transformieren, neue Spalten berechnen)
-
Explorative Analyse
- Daten zusammenfassen (zentrale Tendenz, Streuung, Zusammenhang – jeweils für alle UV und AV sowie weiterer potenziell relevanter Variablen)
- Daten visualisieren (Verteilung der UV, AV, gemeinsame Verteilung von UV und AV)
-
Modellierung und Inferenzstatistik
- Modell berechnen (AV ~ UV1 + UV2 + …)
- Parameter berichten (Punkt- und Intervallschätzer)
- Parameter visualisieren
- Nullhypothesen testen (z. B. ROPE)
- Modellgüte berichten (z. B. R-Quadrat)
10.6.3 Rostlöser
Ihre R-Skills sind etwas eingerostet? Flutscht nicht so? Keine Sorge! Es gibt Rostlöser, der Sie schnell wieder in Schwung bringt. 🧴
10.6.3.1 Grundlagen der Statistik
Das Kursbuch Statistik1 beinhaltet einen Überblick über Datenaufbereitung und -visualierung sowie Modellierung mit dem linearen Modell, alles mit R.
10.6.3.2 Grundlagen der Inferenzstatistik
Das Kursbuch Start:Bayes! stellt einen Einstieg in die Inferenzstatistik mit der Bayes-Statistik bereit.
10.6.3.3 Wie man Umfragedaten auswertet
Hier finden Sie (m)eine Anleitung zur Auswertung von Umfragedaten.
10.7 Überblick zur Statistik
10.7.1 Deskriptiv- vs. Inferenzstatistik
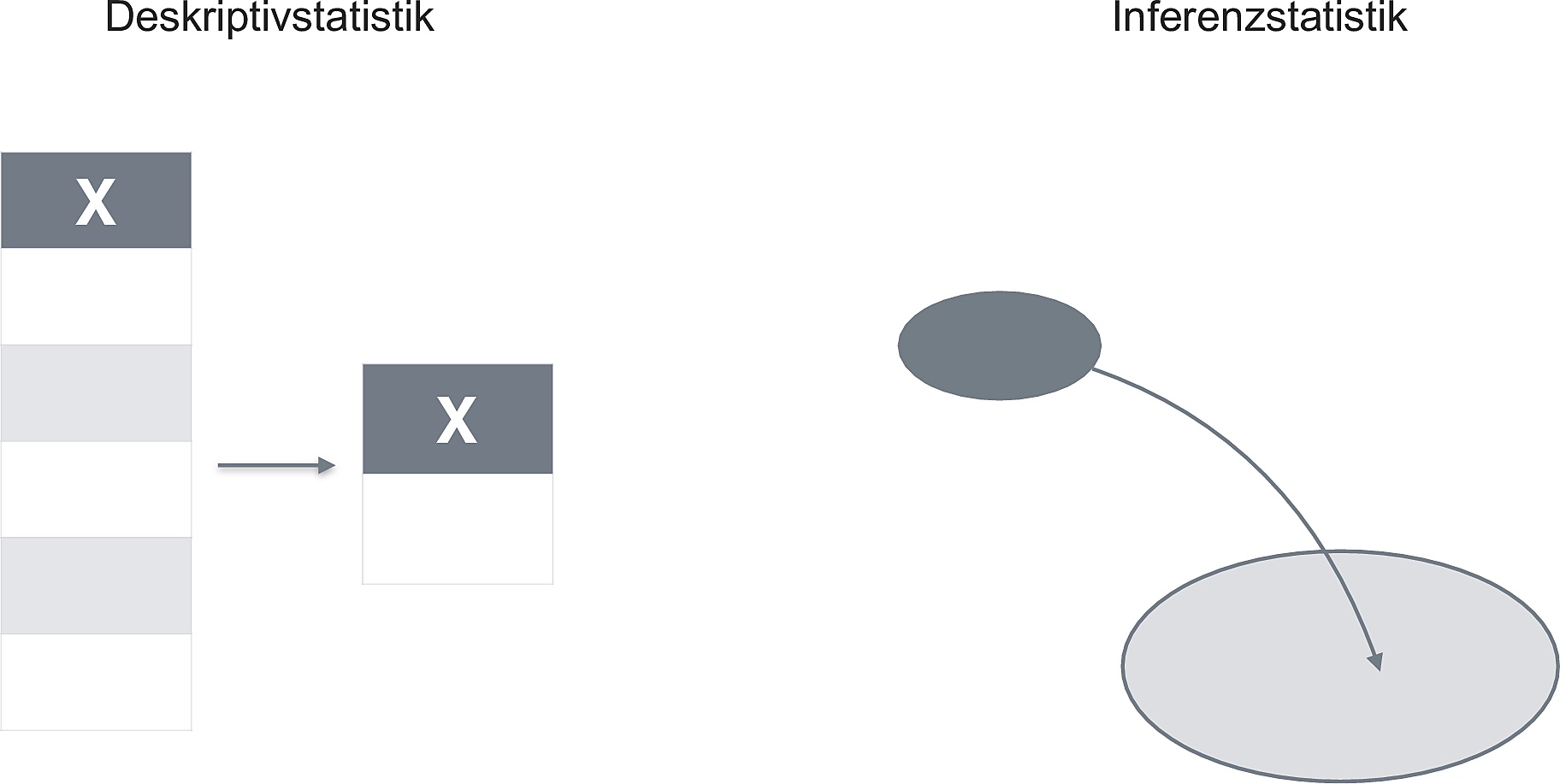
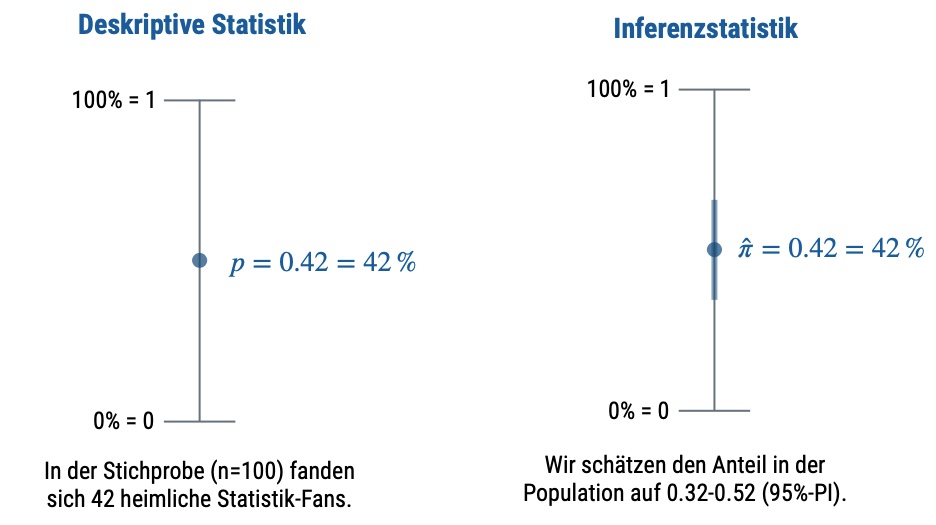
Abbildung 10.3 und Abbildung 10.4 geben einen Überblick zum Unterschied von Deskriptiv- und Inferenzstatistik.
10.7.2 Deskriptivstatistik
Berechnen Sie die relevanten Kennwerte der Deskriptivstatistik für alle Variablen Ihrer Hypothesen (bzw. Forschungsfragen). Das beinhaltet sowohl univariate Analysen (d.h. Kennwerte für eine einzelne Variable) als auch bivariate Analysen (d.h. Zusammenhänge von zwei Variablen, also deren “gemeinsame Verteilung”).
Typische Kennwerte der Deskriptivstatistik sind:
- Arithmetisches Mittel
- Standardabweichung
- Anteil
- Korrelation
- Regressionskoeffizienten
Abbildung 10.5 zeigt interaktive Beispiele für einen Kennwert des Deskriptivstatistik: (lineare) Korrelation1.
plotter is not defined
plotter is not defined
function make_perturbed_graph(f, r, a, b, n) {
let xs = jstat.arange(n).map(() => jstat.uniform.sample(a, b));
let ys = xs.map((x) => f(x) + r());
let plot = plotter({ width: 500, height: 400, grid: false });
jstat.arange(n).forEach((_, i) => plot.point(xs[i], ys[i]));
let R = jstat.corrcoeff(xs, ys);
return html`<div style="text-align:center; width:500px">R = ${d3.format(
"0.4f"
)(R)}</div>${plot.node}`;
}plotter is not defined
import {select as select} from "@jashkenas/inputs"
import {plotter as plotter} from "50dadfdec01c15a8"
import {rk4 as rk4} from "@mcmcclur/runge-kutta-for-systems-of-odes"
import {slider as slider} from "@jashkenas/inputs"
10.7.3 Inferenzstatistik
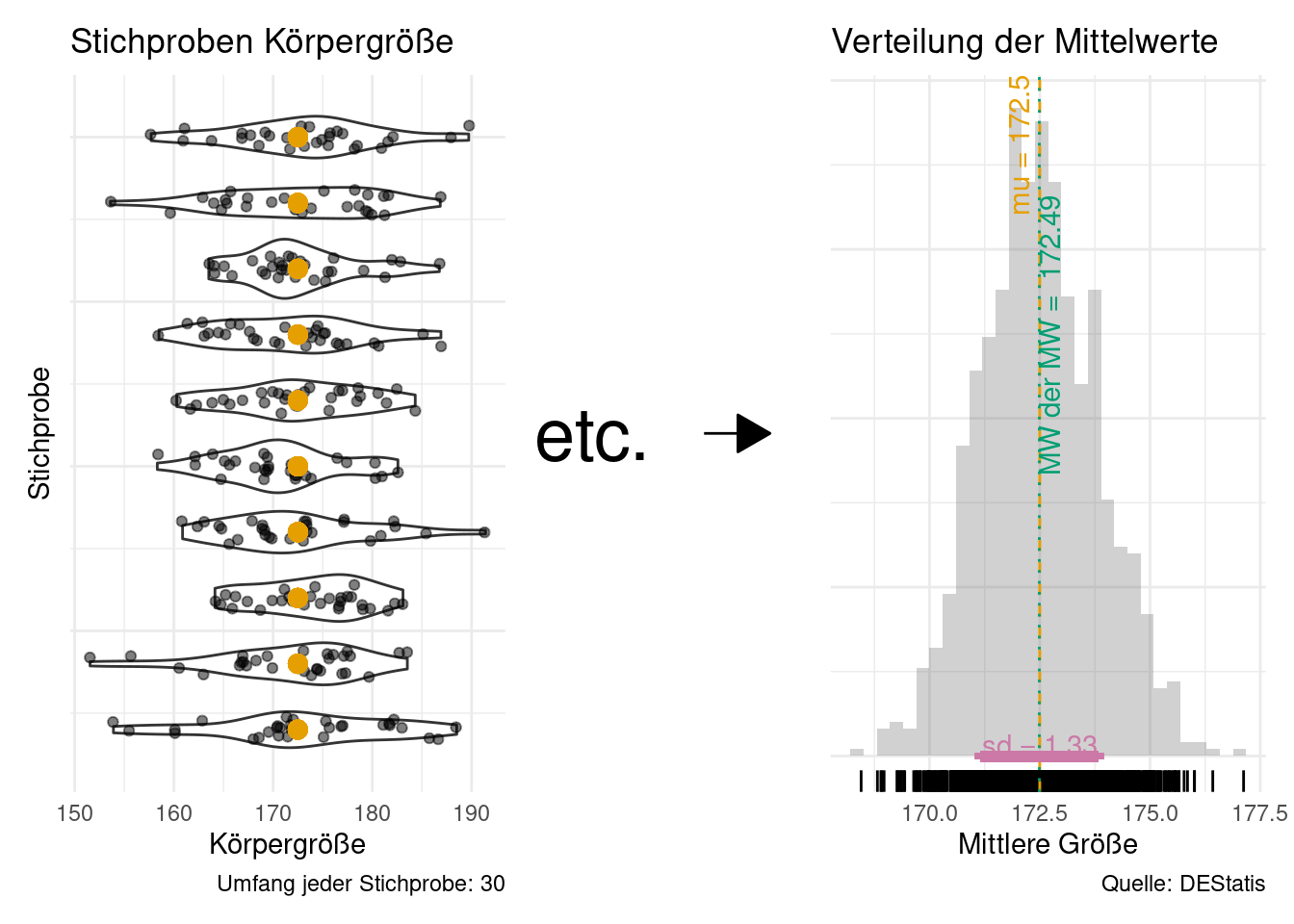
Abbildung 10.6 veranschautlicht die Daaseinsberechtigung der Inferenzstatistik: Eine einzelne Stichprobe schätzt den Mittelwert der Population (mu) ungenau (je kleiner die Stichprobe, desto ungenauer, ceteris paribus). Daher brauchen wir eine Angabe, wie (un)genau unser Mittelwert wohl den “wahren” Mittelwert der Population (mu) schätzt. Genau das macht die Inferenzstatistik!
10.7.4 Modellieren
Definition 10.1 (Modell) Ein Modell ist ein vereinfachtes Abbild der Wirklichkeit.
Der Nutzen eines Modells ist, einen (übermäßig) komplexen Sachverhalt zu vereinfachen oder überhaupt erst handhabbar zu machen. Man versucht zu vereinfachen, ohne Wesentliches wegzulassen. Der Speck muss weg, sozusagen. Das Wesentliche bleibt.
Auf die Statistik bezogen heißt das, dass man einen Datensatz dabei so zusammenfasst, damit man das Wesentliche erkennt. Was ist das “Wesentliche”? Oft interessiert man sich für die Ursachen eines Phänomens. Etwa: “Wie kommt es bloß, dass ich ohne zu lernen die Klausur so gut bestanden habe?”2 Noch allgemeiner ist man dabei häufig am Zusammenhang von X und Y interessiert, s. Abbildung 10.7, die ein Sinnbild von statistischen Modellen widergibt.
10.8 Skriptbasierte vs. klickbasierte Software zur Datenanalyse
Man kann grob zwei Arten von Software-Programmen für Datenanalyse unterscheiden:
- Skriptbasierte: Man schreibt seine Befehle in einer Programmiersprache (z. B. R)
- Klickbasierte: Man klickt in einer Gui, um Befehle auszulösen (z. B. Jamovi)
Die gängigen Beispiele für skriptbasierte Software für Datenanalyse sind R und Python.
Einige empfehlenswerte(re) Programme für die klickbasierte Datenanalyse sind:
Im Folgenden sind die Vorteile der oben genannten klickbasierten Software-Programmen den Vorteilen der oben genannten skriptbasierten Software-Programmen gegenüber gestellt
10.8.1 Vorteile klickbasierter Software

![]()
![]()
- eher kostenlos (es gibt kostenpflichtige Premium-Versionen wie Jamovi Cloud)
- aktuell
- flachere Lernkurve
- R-Code integriert
Beispiele: JASP, Jamovi, Exploratory
10.9 Deskriptivstatistik in der Praxis
Die Deskriptivstatistik fasst eine Datenreihe zu einer Kennzahl zusammen. Der Nutzen liegt im Überblick, den man so gewinnt.
Wir analysieren den Datensatz extra, s. zu Beginn dieses Kapitels, Kapitel 10.1.3. Damit es einfach bleibt, begrenzen wir uns im Folgenden auf ein paar Variablen.
Sagen wir, das sind die Variablen, die uns interessieren:
10.9.1 Deskriptive Ergebnisse für metrische Variablen
Sie können deskriptive Ergebnisse (Ihrer relevanten Variablen) für metrische Variablen z. B. so darstellen, s. Listing 10.1.
| Variable | Mean | SD | IQR | Min | Max | Skewness | Kurtosis | n | n_Missing |
|---|---|---|---|---|---|---|---|---|---|
| n_facebook_friends | 532.61 | 3704.48 | 300.0 | 0.0 | 96055 | 25.67 | 662.76 | 671 | 155 |
| n_hangover | 9.47 | 30.72 | 9.0 | 0.0 | 738 | 17.54 | 399.53 | 800 | 26 |
| age | 25.50 | 5.75 | 6.0 | 18.0 | 54 | 1.81 | 4.39 | 813 | 13 |
| extra_single_item | 2.79 | 0.86 | 1.0 | 1.0 | 4 | -0.27 | -0.60 | 816 | 10 |
| n_party | 17.38 | 19.32 | 19.0 | 0.0 | 150 | 3.27 | 16.10 | 793 | 33 |
| extra_mean | 2.89 | 0.45 | 0.6 | 1.2 | 4 | -0.43 | -0.11 | 822 | 4 |
Übersetzen wir Listing 10.1 vom Errischen ins Deutsche:
- Hey R,
- nimm die Tabelle
extra… und dann - wähle jede Variable, die ich im Vektor
extra_corr_namesangegeben habe … und dann - beschreibe die Verteilung (jeweils, also für jede Variable) … und dann
- mache aus der drögen Tabelle eine schicke. Fertig!
kable() macht aus dem drögen Output in der R-Konsole eine schicke HTML-Tabelle3, wenn man das Quarto-Dokument rendert.
Statt select(any_of(extra_corr_names)) könnten Sie natürlich auch schreiben select(n_facebook_friends, ...), wobei Sie für die drei Punkte alle Variablen von Interesse nennen würden.
Praktischerweise kann man describe_distribution auch für gruppierte Datensätze nutzen, um so gruppierte Verteilungsmaße zu bekommen:
extra |>
group_by(sex) |>
describe_distribution(extra_mean)sex <fct> | Variable <chr> | Mean <dbl> | SD <dbl> | IQR <dbl> | Min <dbl> | Max <dbl> | Skewness <dbl> | |
|---|---|---|---|---|---|---|---|---|
| Frau | extra_mean | 2.908705 | 0.4219142 | 0.6 | 1.6 | 3.9 | -0.3380531 | |
| Mann | extra_mean | 2.861772 | 0.4989651 | 0.7 | 1.2 | 4.0 | -0.4812037 |
10.9.2 Visualisierung von metrischen Variablen
10.9.2.1 Univariat
Mit dem R-Paket ggpubr kann man ansprechende Visualisierungen erzeugen, und zwar ziemlich einfach. Mit help(ggpubr) bekommen Sie Einblick in die Hilfeseite von ggpubr.
gghistogram(extra, x = "extra_mean", add = "mean") +
labs(x = "Extraversion (Mittelwert)",
y = "Häufigkeit",
caption = "Die gestrichelte horizontale Linie zeigt den Mittelwert der Verteilung.")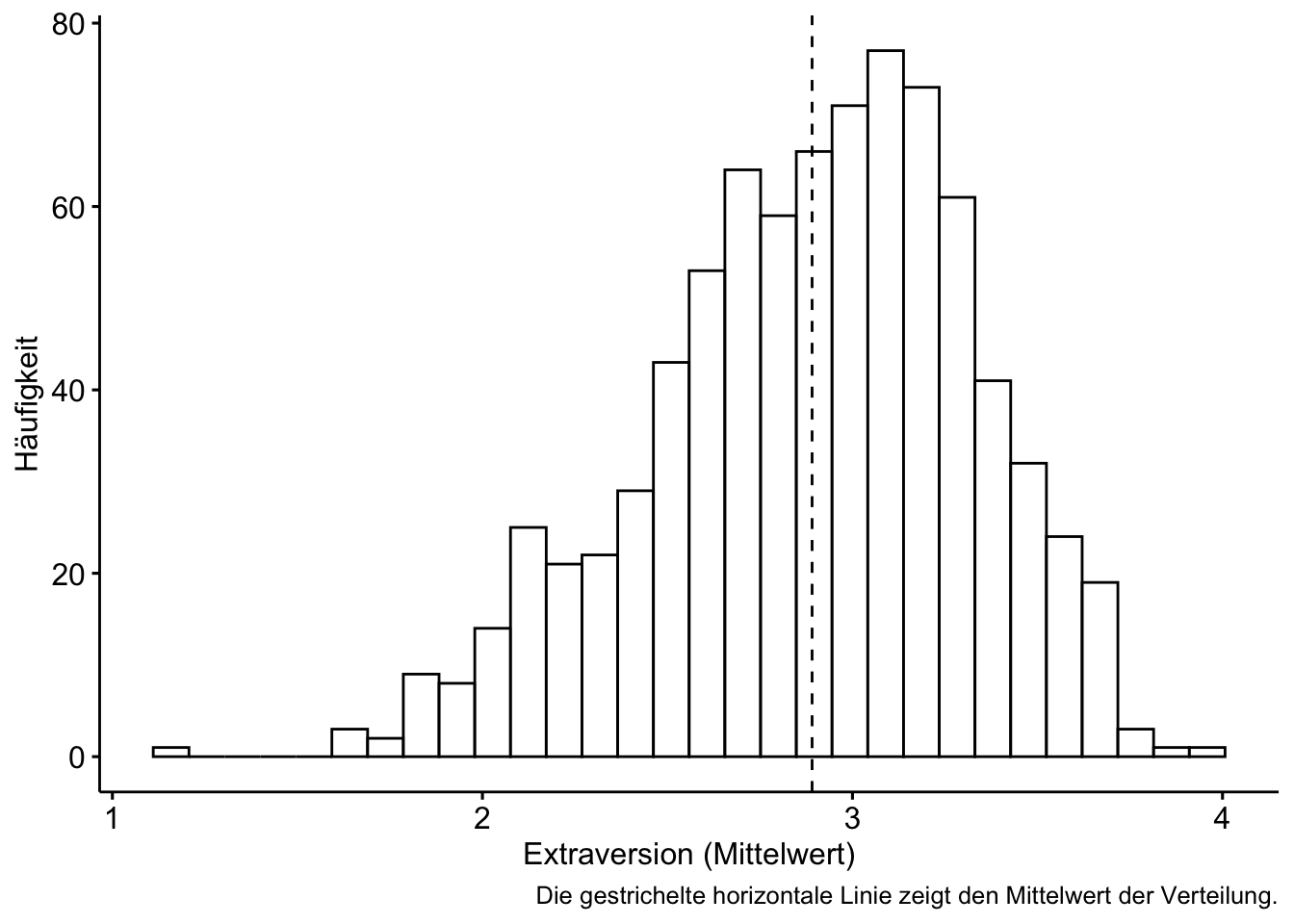
10.9.2.2 Gruppenvergleich
Vergleicht man die Verteilung einer Variablen unterteilt auf die Stufen (Gruppen) einer zweiten Variablen, so untersucht man die gemeinsame Verteilung dieser beiden Variablen.
Es gibt verschiedene Methoden, Gruppenunterschiede zu verdeutlichen. Man könnte z. B. pro Gruppe ein Histogramm zeigen, das ist recht informationsreich.
extra_no_na <-
extra |>
filter(sex == "Frau" | sex == "Mann")
gghistogram(extra_no_na, x = "extra_mean", add = "mean", facet.by = "sex") +
labs(x = "Extraversion (Mittelwert)",
y = "Häufigkeit",
caption = "Die gestrichelte horizontale Linie zeigt den Mittelwert der Verteilung.")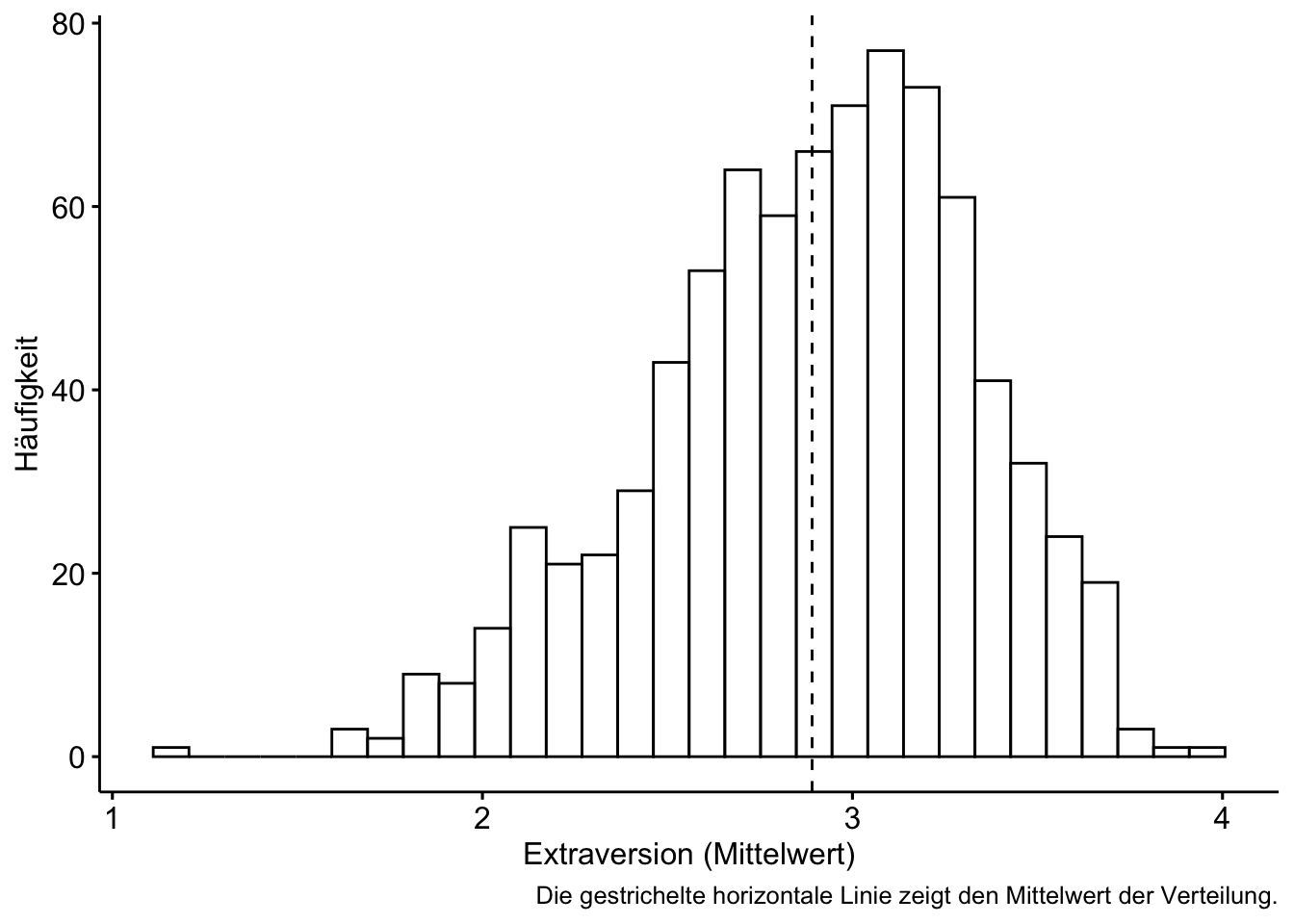
Gerade bei vielen Gruppen kann aber ein Boxplot übersichtlicher sein.
extra_no_na |>
ggboxplot(y = "extra_mean", x = "sex")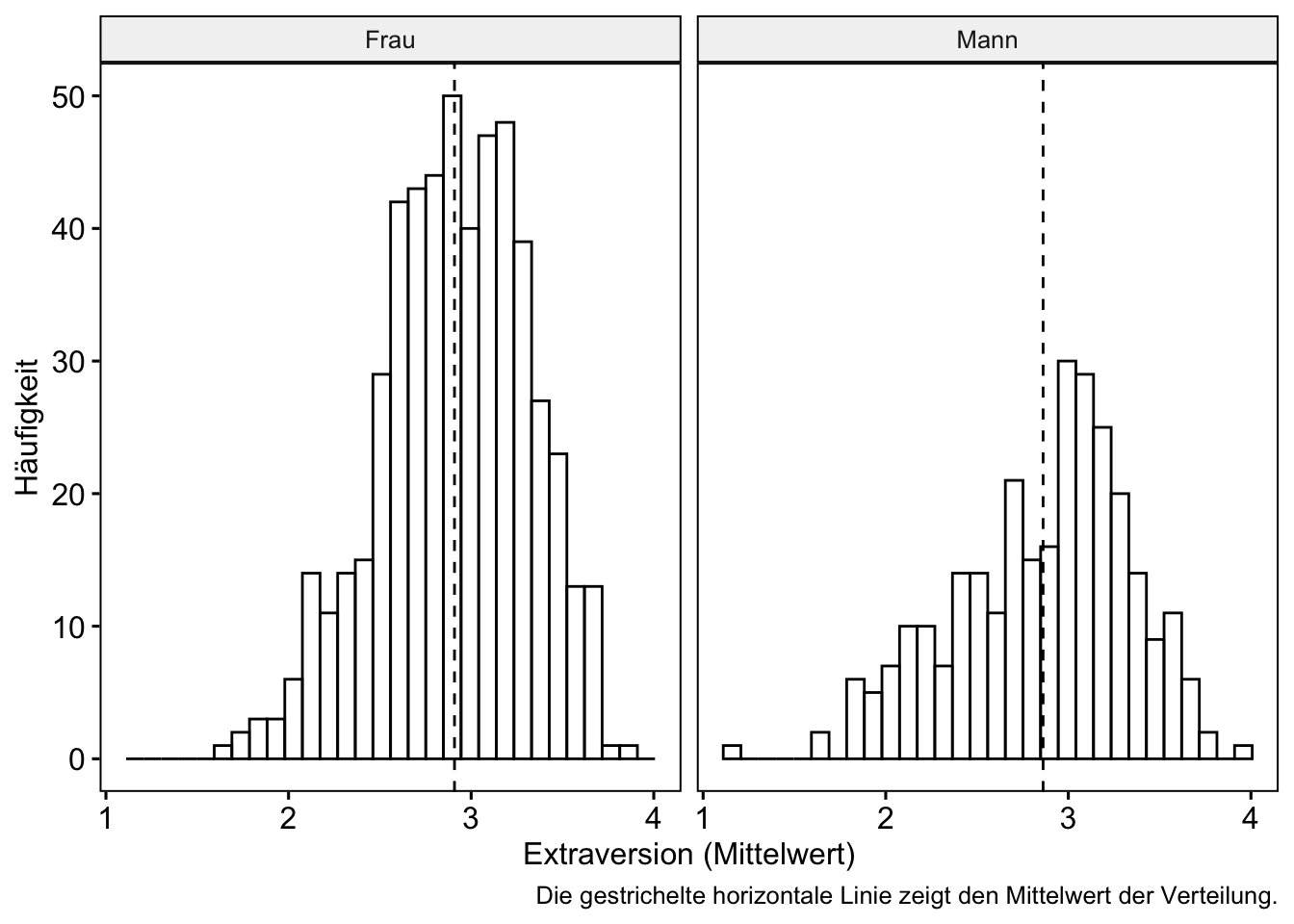
10.9.3 Deskriptive Ergebnisse für nominale Variablen
10.9.3.1 Univariate Häufigkeiten
Lassen wir uns die Häufigkeiten für sex und für smoker ausgeben, also für jede Variable separat (univariat).
Mit tidyverse kann man das in vertrauter Manier bewerkstelligen:
extra |>
count(sex)sex <chr> | n <int> | |||
|---|---|---|---|---|
| Frau | 529 | |||
| Mann | 286 | |||
| NA | 11 |
Etwas schicker sieht es aus mit data_tabulate aus easystats:
extra |>
select(sex) |>
#drop_na() |> ggf. ohne fehlende Werte
data_tabulate() |>
print_md() # erstelle eine schicke HTML-Tabelle| Value | N | Raw % | Valid % | Cumulative % |
|---|---|---|---|---|
| Frau | 529 | 64.04 | 64.91 | 64.91 |
| Mann | 286 | 34.62 | 35.09 | 100.00 |
| (NA) | 11 | 1.33 | (NA) | (NA) |
total N=826 valid N=815
Zur Visualisierung von Häufigkeiten bieten sich Balkendiagramme an. Nutzt man ggpubr muss man zuerst selber die Anzahl der Werte auszählen (lassen), das geht z. B. mit count.
extra_no_na |>
count(sex)sex <chr> | n <int> | |||
|---|---|---|---|---|
| Frau | 529 | |||
| Mann | 286 |
10.9.3.2 Bivariate Häufigkeiten
Wir können uns auch die bivariaten Häufigkeiten ausgeben lassen: Betrachten wir die Geschlechtsverteilung bei Menschen, die (nicht) jünger als 20 Jahre sind:
| Variable | Group | Value | N | Raw % | Valid % | Cumulative % |
|---|---|---|---|---|---|---|
| sex | age > 20 (FALSE) | Frau | 89 | 74.17 | 74.17 | 74.17 |
| Mann | 31 | 25.83 | 25.83 | 100.00 | ||
| (NA) | 0 | 0.00 | (NA) | (NA) | ||
| sex | age > 20 (TRUE) | Frau | 437 | 63.43 | 63.43 | 63.43 |
| Mann | 252 | 36.57 | 36.57 | 100.00 | ||
| (NA) | 0 | 0.00 | (NA) | (NA) | ||
extra |>
drop_na(age, sex) |> # fehlende Werte entfernen
count(young = age < 20, sex) |>
ggbarplot(x = "young", y = "n", fill = "sex")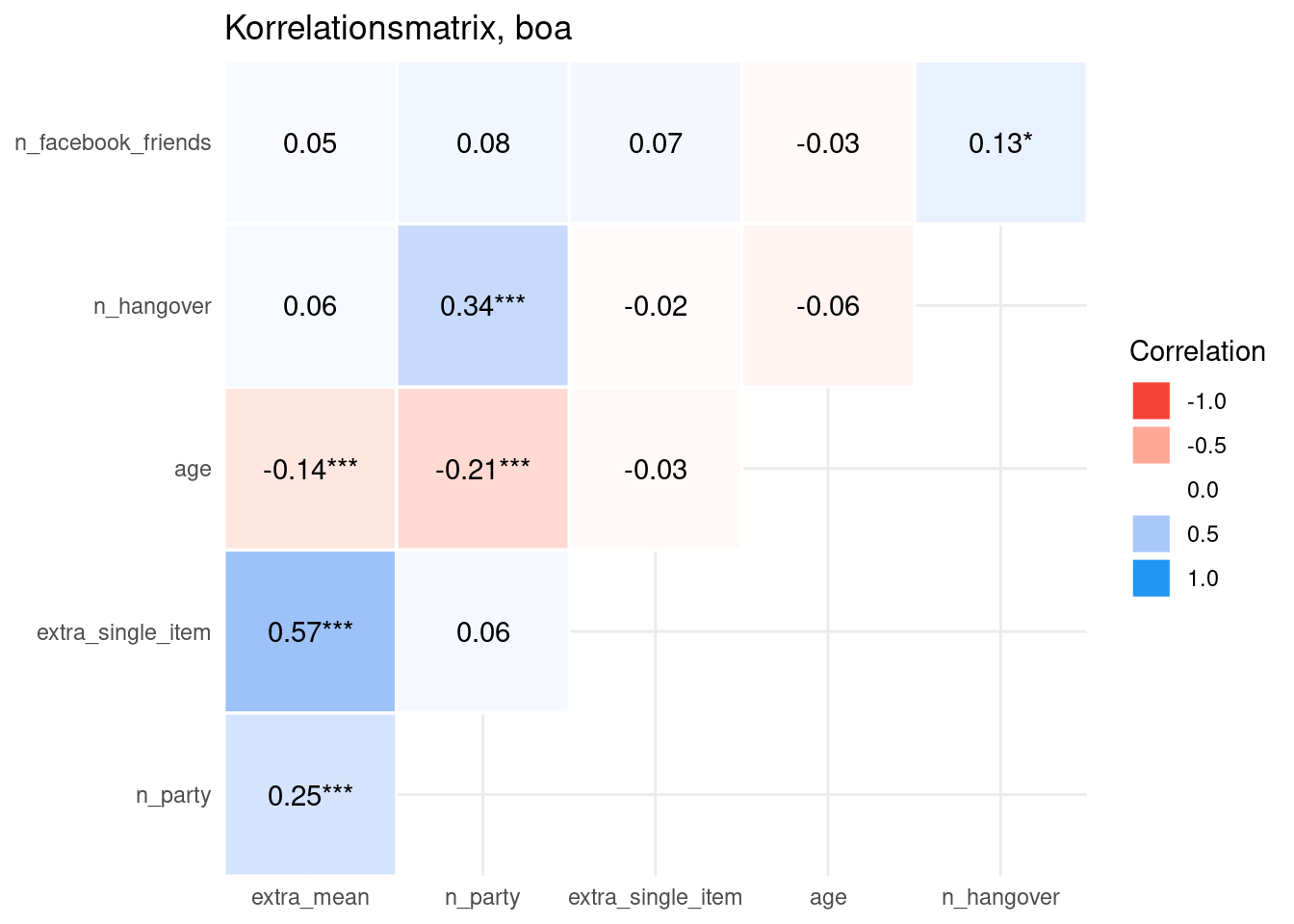
Eicht man die Höhen der Balken auf 100%, so kann man Zusammenhänge gut visualisieren.
extra |>
drop_na(age, sex) |> # fehlende Werte entfernen
count(young = age < 20, sex) |>
ggbarplot(x = "young", y = "n", fill = "sex",
position = position_fill()) +
labs(title = "Deutlicher Zusammenhang zwischen Geschlecht und Alter")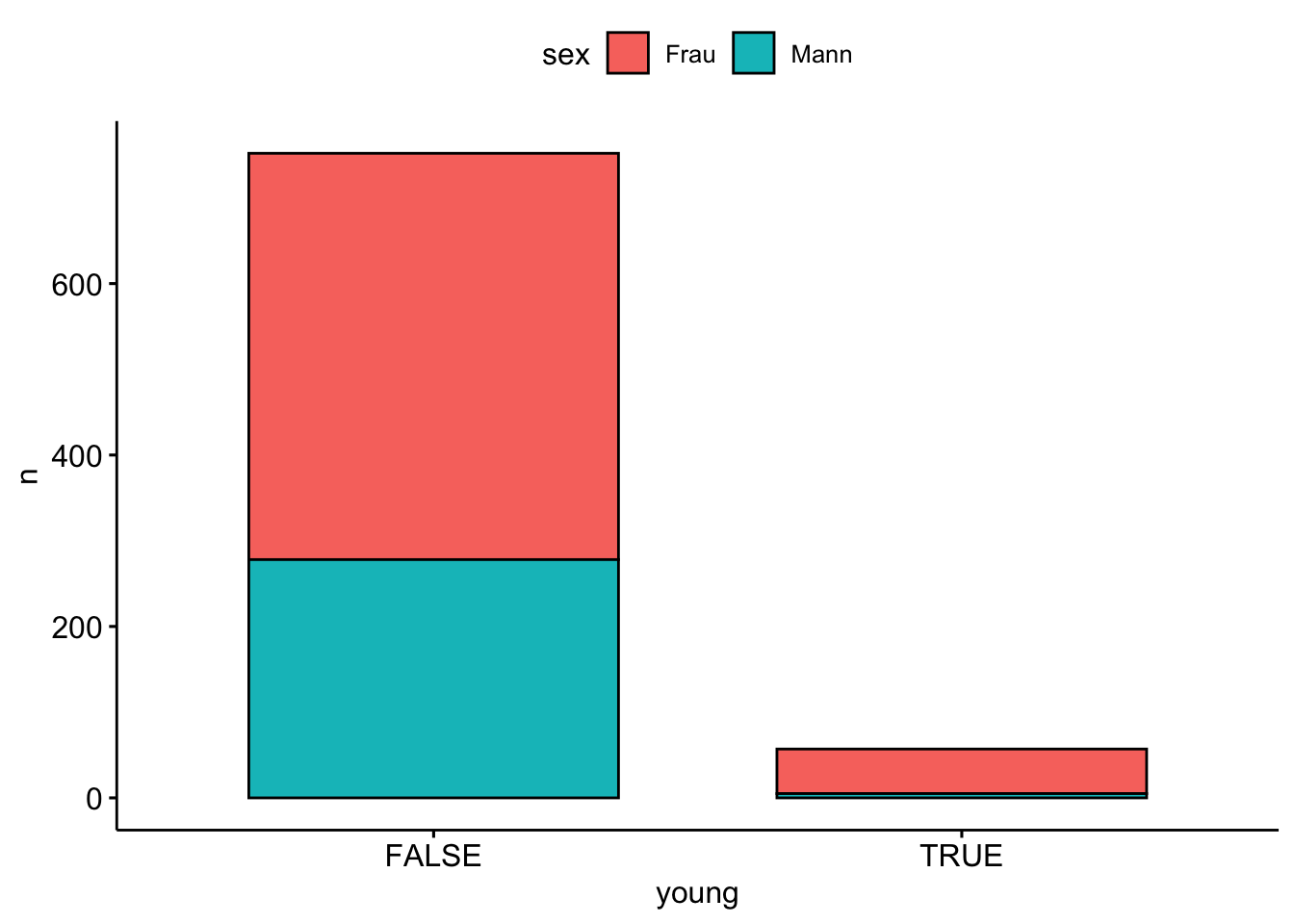
extra |>
drop_na(n_party, sex) |> # fehlende Werte entfernen
count(party_tiger = n_party > 5, sex) |>
ggbarplot(x = "party_tiger", y = "n", fill = "sex",
position = position_fill()) +
labs(title = "Schwacher Zusammenhang zwischen Geschlecht und 'Party_Tiger'")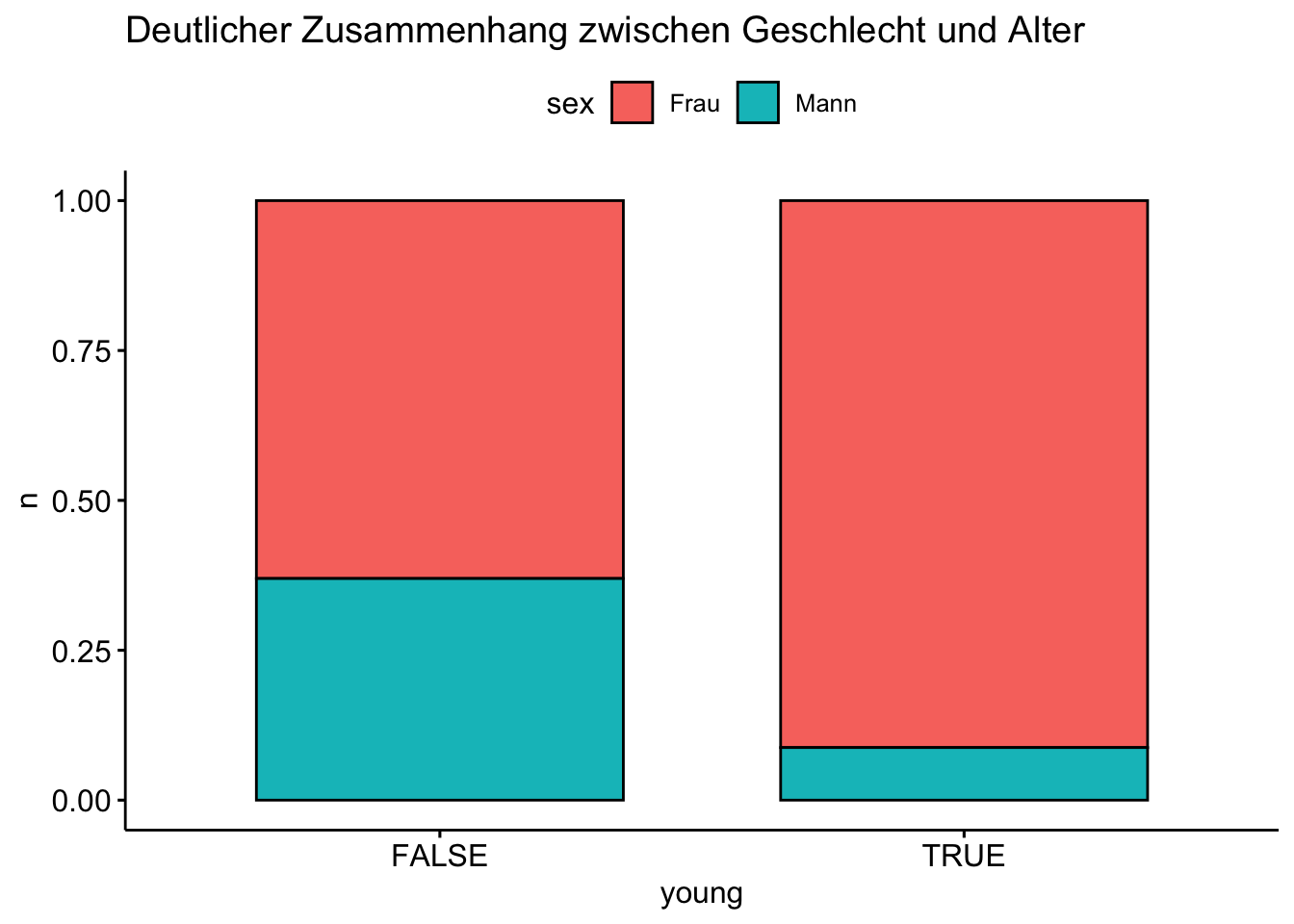
10.9.4 Korrelationen darstellen
In einer Umfrage erhebt man häufig mehrere Variablen, ein Teil davon oft Konstrukte. Es bietet sich in einem ersten Schritt an, die Korrelationen dieser Variablen untereinander darzustellen.
10.9.4.1 Korrelationsmatrix
| Parameter | extra_mean | n_party | extra_single_item | age | n_hangover |
|---|---|---|---|---|---|
| n_facebook_friends | 0.05 | 0.08 | 0.07 | -0.03 | 0.13 |
| n_hangover | 0.06 | 0.34 | -0.02 | -0.06 | NA |
| age | -0.14 | -0.21 | -0.03 | NA | NA |
| extra_single_item | 0.57 | 0.06 | NA | NA | NA |
| n_party | 0.25 | NA | NA | NA | NA |
Sie möchten das Ergebnis als normalen R-Dataframe? Sie haben keine Lust auf dieses Rumgetue, sondern wollen das lieber als selber geradeziehen. Also gut:
cor_results <-
extra %>%
select(any_of(extra_corr_names)) %>%
correlation() %>%
summary() |>
print_md() # erstelle schicke HTML-Tabelle
cor_results| Parameter | extra_mean | n_party | extra_single_item | age | n_hangover |
|---|---|---|---|---|---|
| n_facebook_friends | 0.05 | 0.08 | 0.07 | -0.03 | 0.13* |
| n_hangover | 0.06 | 0.34*** | -0.02 | -0.06 | |
| age | -0.14*** | -0.21*** | -0.03 | ||
| extra_single_item | 0.57*** | 0.06 | |||
| n_party | 0.25*** |
p-value adjustment method: Holm (1979)
Man kann sich die Korrelationsmatrix auch in der Bayes-Geschmacksrichtung ausgeben lassen:
extra %>%
select(any_of(extra_corr_names)) %>%
correlation(bayesian = TRUE) %>%
summary() %>%
kable(digits = 2)| Parameter | extra_mean | n_party | extra_single_item | age | n_hangover |
|---|---|---|---|---|---|
| n_facebook_friends | 0.05 | 0.08 | 0.07 | -0.03 | 0.13 |
| n_hangover | 0.06 | 0.33 | -0.02 | -0.06 | NA |
| age | -0.14 | -0.21 | -0.03 | NA | NA |
| extra_single_item | 0.57 | 0.06 | NA | NA | NA |
| n_party | 0.25 | NA | NA | NA | NA |
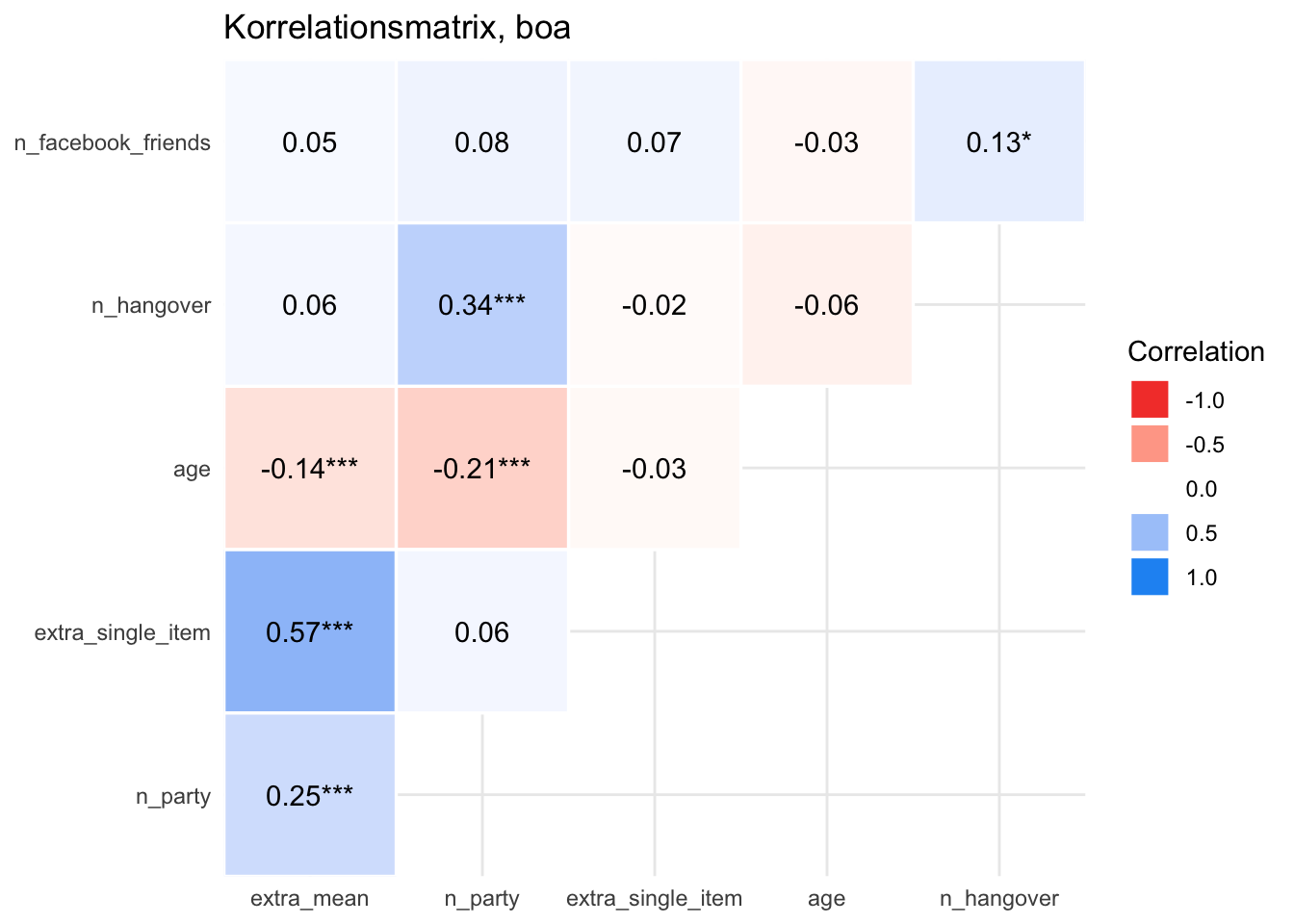
10.9.4.2 Korrelationsmatrizen visualisieren
Viele R-Pakete bieten sich an. Nehmen wir easystats.
10.10 Aufgaben
Auf dem Datenwerk finden Sie eine Anzahl an Aufgaben zum Thema Datenanalyse. Schauen Sie sich mal die folgenden Tags an:
10.11 Fallstudien
Fallstudien zur explorativen Datenanalyse (EDA; d.h. deskriptive Statistik und Datenvisualisierung) finden Sie z. B. im Datenwerk: